题目内容
16.已知函数$f(x)=alnx+\frac{{2{a^2}}}{x}+x({a∈R})$.(1)当a=1时,讨论函数y=f(x)的单调性;
(2)若对任意m,n∈(0,2)且m≠n,有$\frac{f(m)-f(n)}{m-n}<1$恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)令g(x)=f(x)-x=alnx+$\frac{{2a}^{2}}{x}$,通过讨论m,n的大小,得到g(x)在(0,2)上单调递减,通过讨论a的范围,确定函数g(x)的单调性,从而确定a的具体范围即可.
解答 解:(1)函数的定义域为(0,+∞),
a=1时,f(x)=lnx+$\frac{2}{x}$+x,f′(x)=$\frac{1}{x}$-$\frac{2}{{x}^{2}}$+1=$\frac{{x}^{2}+x-2}{{x}^{2}}$=$\frac{(x+2)(x-1)}{{x}^{2}}$,
令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
故f(x)在(0,1)递减,在(1,+∞)递增;
(2)若m>n,由$\frac{f(m)-f(n)}{m-n}<1$,
得f(m)-m<f(n)-n
若m<n,由$\frac{f(m)-f(n)}{m-n}<1$,
得f(m)-m>f(n)-n
令g(x)=f(x)-x=alnx+$\frac{{2a}^{2}}{x}$,
g′(x)=$\frac{a(x-2a)}{{x}^{2}}$(x>0)
∵g(x)在(0,2)上单调递减,
∴①当a=0时,g′(x)=0,不符合题意;
②当a>0时,由g′(x)<0得0<x<2a,
所以g(x)在(0,2a)上递减,
所以2≤2a,即a≥1;
③当a<0时,在(0,+∞)上,都有g′(x)<0,
所以g(x)在(0,+∞)上递减,即在(0,2)上也单调递减,
综上,实数a的取值范围为(-∞,0)∪[1,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.指数函数y=ax(a>0,a≠1)的反函数图象过点(9,2),则a=( )
| A. | 3 | B. | 2 | C. | 9 | D. | 4 |
7.已知F1、F2分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的左右两个焦点,过F1作倾斜角为$\frac{π}{4}$的弦AB,则△F2AB的面积为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$-1 |
1.若实数x,y满足$\left\{\begin{array}{l}3x-y-9≥0\\ x-y-3≤0\\ y≤3\end{array}\right.$,则使得z=y-2x取得最大值的最优解为( )
| A. | (3,0) | B. | (3,3) | C. | (4,3) | D. | (6,3) |
8.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$2\sqrt{3}$,AB=2,AC=1,∠BAC=60°,则此球的表面积等于( )
| A. | 5π | B. | 20π | C. | 8π | D. | 16π |
6. 如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )
如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )
 如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )
如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是( )| A. | 平行 | B. | 相交成60° | C. | 相交且垂直 | D. | 异面直线 |
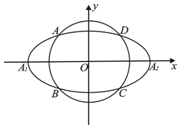 如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.