题目内容
已知函数 (
( ).(Ⅰ)当
).(Ⅰ)当 时,求
时,求 的图象在
的图象在 处的切线方程;(Ⅱ)若函数
处的切线方程;(Ⅱ)若函数 在
在 上有两个零点,求实数
上有两个零点,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 的图象与
的图象与 轴有两个不同的交点
轴有两个不同的交点 ,且
,且 ,
,
求证: (其中
(其中 是
是 的导函数).
的导函数).
(Ⅰ)当 时,
时, ,
, ,切点坐标为
,切点坐标为 ,
,
切线的斜率 ,则切线方程为
,则切线方程为 ,即
,即 . 2分
. 2分
(Ⅱ) ,则
,则 ,
,
∵ ,故
,故 时,
时, .当
.当 时,
时, ;当
;当 时,
时, .
.
故 在
在 处取得极大值
处取得极大值 . 4分
. 4分
又 ,
, ,
, ,则
,则 ,
,
∴ 在
在 上的最小值是
上的最小值是 . 6分
. 6分
 在
在 上有两个零点的条件是
上有两个零点的条件是 解得
解得 ,
,
∴实数 的取值范围是
的取值范围是 . 8分
. 8分
(Ⅲ)∵ 的图象与
的图象与 轴交于两个不同的点
轴交于两个不同的点 ,
,
∴方程 的两个根为
的两个根为 ,则
,则 两式相减得
两式相减得 .又
.又 ,
, ,则
,则
 .
.
下证 (*),即证明
(*),即证明 ,
, ,
,
∵ ,∴
,∴ ,即证明
,即证明 在
在 上恒成立. 10分
上恒成立. 10分
∵ ,又
,又 ,∴
,∴ ,
,
∴ 在
在 上是增函数,则
上是增函数,则 ,从而知
,从而知 ,
,
故(*)式<0,即 成立
成立

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知定义在R上的偶函数f(x)满足f(1+x)=f(1﹣x),且x∈[0,1]时, ,则方程
,则方程 在区间[﹣3,3]上的根的个数为( )
在区间[﹣3,3]上的根的个数为( )
|
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
 -sin2α的结果是________.
-sin2α的结果是________. 的值为________.
的值为________. .记
.记
 的周期;
的周期; ABC中,角A、B、C的对边分别是a、b、c,且满足(2a—c)
ABC中,角A、B、C的对边分别是a、b、c,且满足(2a—c) B=b
B=b , 若
, 若 ,试判断
,试判断
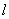 和双曲线
和双曲线 相交于
相交于 、
、 两点,线段
两点,线段 的中点为
的中点为 (与坐标原点
(与坐标原点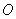 不
不 ,直线
,直线 的斜率为
的斜率为 ,则
,则
 B.
B. C.
C. D.
D.
