题目内容
已知集合A={1,2,3,4,5},若x,y,z∈A,则x,y,z成等差数列的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:由排列公式求出基本事件的总数,再按公差的大小依次列举出所求事件包含的基本事件,最后代入古典概型下的概率公式求值即可.
解答:
解:由题意得,集合A={1,2,3,4,5},若x,y,z∈A,
所以x,y,z构成数列共:5×5×5=125,
设事件A:x,y,z成等差数列,则事件A包含的基本事件为:
公差为0:(1,1,1),(2,2,2),…,(5,5,5)共5种,
公差为1或-1:(1,2,3),(2,3,4),(3,4,5),…共6种,
公差为2或-2:(1,3,5),(5,3,1)共2种,
一共5+6+2=13种,
所以P(A)=
,
故选:A.
所以x,y,z构成数列共:5×5×5=125,
设事件A:x,y,z成等差数列,则事件A包含的基本事件为:
公差为0:(1,1,1),(2,2,2),…,(5,5,5)共5种,
公差为1或-1:(1,2,3),(2,3,4),(3,4,5),…共6种,
公差为2或-2:(1,3,5),(5,3,1)共2种,
一共5+6+2=13种,
所以P(A)=
| 13 |
| 125 |
故选:A.
点评:本题考查排列公式,等差数列的定义,以及古典概型下的概率公式的应用,注意列基本事件时按一定的顺序一一列出,做到不重不漏.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
若点P(m,n)Q(n-1,m+1)关于直线l对称,则l的方程是( )
| A、x-y+1=0 |
| B、x-y=0 |
| C、x+y+1=0 |
| D、x+y=0 |
设
、
、
是任意的非零平面向量,且相互不共线,则:
①(
•
)
-(
•
)
=
; ②|
|-|
|<|
-
|③(
•
)
-(
•
)
不与
垂直; ④(3
+2
)•(3
-2
)=9|
|2-4|
|2中,是真命题的有( )
| a |
| b |
| c |
①(
| a |
| b |
| c |
| c |
| a |
| b |
| 0 |
| a |
| b |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、②④ |
若a<b<0,则下列不等式中不能成立的是( )
A、
| ||||
B、
| ||||
| C、|a|>|b| | ||||
| D、a2>b2 |
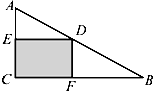 在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.
在RT△ABC中,直角边AC=3,BC=4,点D是斜边AB上的动点,DE⊥AC交AC于点E,DF⊥BC交BC于点F,设CE=x.