题目内容
20.已知函数f(x)=lnx+ax2(1)讨论f(x)的单调性;
(2)设a>1,若对任意x1,x2∈(0,+∞),恒有|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围.
分析 (1)先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求出单调区间.
(2)根据第一问的单调性先对|f(x1)-f(x2)|≥4|x1-x2|进行化简整理,转化成研究g(x)=f(x)-4x在(0,+∞)单调增函数,再利用参数分离法求出a的范围.
解答 解:(1)f(x)的定义域是(0,+∞),
f′(x)=$\frac{2{ax}^{2}+1}{x}$,(x>0),
a≥0时,f′(x)>0,故f(x)在(0,+∞)递增,
a<0时,令f′(x)>0,解得:0<x<$\sqrt{-\frac{1}{2a}}$,
令f′(x)<0,解得:x>$\sqrt{-\frac{1}{2a}}$,
故函数f(x)在(0,$\sqrt{-\frac{1}{2a}}$)递增,在($\sqrt{-\frac{1}{2a}}$,+∞)递减;
(2)不妨设x1≤x2,而a>1,
由(1)得:f(x)在(0,+∞)递增,
从而对任意x1,x2∈(0,+∞),|f(x1)-f(x2)|≥4|x1-x2|
等价于?x1,x2∈(0,+∞),f(x2)-4x2≥f(x1)-4x1①
令g(x)=f(x)-4x,则g′(x)=$\frac{1}{x}$+2ax-4
①等价于g(x)在(0,+∞)单调递增,即$\frac{1}{x}$+2ax-4≥0.
从而2a≥$\frac{4}{x}-\frac{1}{{x}^{2}}$=$-(\frac{1}{x}-2)^{2}$+4,∴a≥2
故a的取值范围为[2,+∞).
点评 本小题主要考查函数的导数,单调性,极值,不等式等基础知识,考查综合利用数学知识分析问题、解决问题的能力.

练习册系列答案
相关题目
11.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为( )
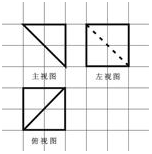

| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | 4$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
8.已知{an}是等比数列,a2=2,a5=$\frac{1}{4}$,则a1a2+a2a3+…+anan+1=( )
| A. | 16(1-4-n) | B. | 16(1-2-n) | C. | $\frac{32}{3}(1-{4^{-n}})$ | D. | $\frac{32}{3}(1-{2^{-n}})$ |
5.已知集合M={x|x2>4},N={-3,-2,2,3,4},则M∩N=( )
| A. | {3,4} | B. | {-3,3,4} | C. | {-2,3,4} | D. | {-3,-2,2,3,4} |
12.已知奇函数f(x)满足,x>0时,f(x)=x2-2x;则x<0时,f(x)的解析式为( )
| A. | -x2-2x | B. | -x2+2x | C. | x2-2x | D. | x2+2x |