题目内容
10.已知二次函数f(x)=x2-16x+q+3(1)当q=1时,求f(x)在[-1,9]上的值域;
(2)问:是否存在常数q(0<q<10),使得当x∈[q,10]时,f(x)的最小值为-51?若存在,求出q的值,若不存在,说明理由.
分析 (1)计算f(x)的对称轴,判断f(x)的单调性,从而求出f(x)的值域;
(2)对q进行讨论判断f(x)在[q,10]上的单调性,令fmin(x)=-51解出q.
解答 解:(1)q=1时,f(x)=x2-16x+4=(x-8)2-60.
∴f(x)在区间[-1,8]上递减,在区间[8,9]上递增,
∴f(x)max=f(-1)=21,f(x)min=f(8)=-60,
∴f(x)在[-1,9]上的值域为[-60,21].
(2)假设存在常数q(0<q<10),使得当x∈[q,10]时,f(x)的最小值为-51,
∵f(x)=x2-16x+q+3=(x-8)2+q-61,x∈[q,10]
∴当0<q<8时,f(x)min=f(8)=q-61=-51,∴q=10(舍).
当q≥8时,f(x)在区间[q,10]上单调递增,$f{(x)_{min}}={q^2}-15q+3=-51$,
解得q=6(舍)或q=9,
故存在常数q=9,使得当x∈[q,10]时,f(x)的最小值为-51.
点评 本题考查了二次函数的单调性,分类讨论思想,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15.某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
| 年龄(岁) | 频率 | |
| 第1组 | [25,30) | 0.1 |
| 第2组 | [30,35) | 0.1 |
| 第3组 | [35,40) | 0.4 |
| 第4组 | [40,45) | 0.3 |
| 第5组 | [45,50] | 0.1 |
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
2.f(x)是定义在(-2,2)上的减函数,若f (m-1)>f(2m-1),则实数m的取值范围是( )
| A. | (0,+∞) | B. | (0,$\frac{3}{2}$) | C. | (-1,3) | D. | ($-\frac{1}{2}$,$\frac{3}{2}$) |
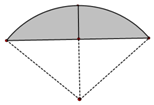 《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.