题目内容
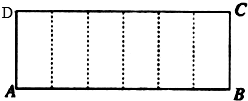
已知矩形 A BCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .

考点:棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:正六棱柱的底面边长为x,高为y,则6x+y=9,0<x<1.5,表示正六棱柱的体积,利用基本不等式求最值,求出正六棱柱的外接球的半径,即可求出外接球的表面积.
解答:
解:设正六棱柱的底面边长为x,高为y,则6x+y=9,0<x<1.5,
正六棱柱的体积V=6×
x2y=
•3x•3x•(9-6x)≤
[
]3=
,
当且仅当x=1时,等号成立,此时y=3,
可知正六棱柱的外接球的球心是其上下底面中心连线的中点,则半径为
=
,
∴外接球的表面积为4π×
=13π.
故答案为:13π.
正六棱柱的体积V=6×
| ||
| 4 |
| ||
| 6 |
| ||
| 6 |
| 3x+3x+(9-6x) |
| 3 |
9
| ||
| 2 |
当且仅当x=1时,等号成立,此时y=3,
可知正六棱柱的外接球的球心是其上下底面中心连线的中点,则半径为
1+
|
| ||
| 2 |
∴外接球的表面积为4π×
| 13 |
| 4 |
故答案为:13π.
点评:本题考查外接球的表面积,考查基本不等式的运用,确定正六棱柱的外接球的半径是关键.

练习册系列答案
相关题目
 某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )
某几何体的三视图如图所示,若其正视图为等腰梯形,侧视图为正三角形,则该几何体的表面积为( )A、2
| ||
B、4
| ||
| C、6 | ||
| D、8 |
一个几何体的三视图如图所示,则该几何体的外接球的表面积为( )
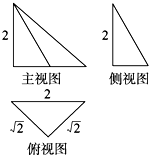

| A、36π | ||
| B、8π | ||
C、
| ||
D、
|
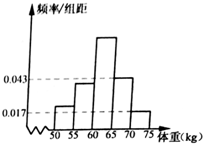 某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频率为11.
某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频率为11.