题目内容
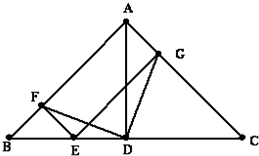如图，在△ABC中，∠BAC=90°，AD是BC边上的高，E是BC边上的一个动点（不与B，C重合），EF⊥AB，EG⊥AC，垂足分别为F，G．
（1）求证
| EG |
| AD |
| CG |
| CD |
（2）FD与DG是否垂直？若垂直，请给出证明；若不垂直，请说明理由；
（3）当AB=AC时，△FDG为等腰直角三角形吗？并说明理由．
考点：相似三角形的判定
专题：立体几何
分析：（1）由比例线段可知，我们需要证明△ADC∽△EGC，由两个角对应相等即可证得；
（2）由矩形的判定定理可知，四边形AFEG为矩形，根据矩形的性质及相似三角形的判定可得到△AFD∽△CGD，从而不难得到结论；
（3）是，利用相似三角形的性质即可求得．
（2）由矩形的判定定理可知，四边形AFEG为矩形，根据矩形的性质及相似三角形的判定可得到△AFD∽△CGD，从而不难得到结论；
（3）是，利用相似三角形的性质即可求得．
解答：
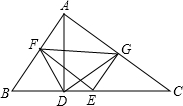证明：（1）在△ADC和△EGC中，
∵∠ADC=∠EGC，∠C=∠C，
∴△ADC∽△EGC．
∴
=
．（3分）
解：（2）FD与DG垂直．（4分）
证明如下：
在四边形AFEG中，
∵∠FAG=∠AFE=∠AGE=90°，
∴四边形AFEG为矩形．
∴AF=EG．
∵
=
，
∴
=
．（6分）
又∵△ABC为直角三角形，AD⊥BC，
∴∠FAD=∠C=90°-∠DAC，
∴△AFD∽△CGD．
∴∠ADF=∠CDG．（8分）
∵∠CDG+∠ADG=90°，
∴∠ADF+∠ADG=90°．
即∠FDG=90°．
∴FD⊥DG．（10分）
（3）当AB=AC时，△FDG为等腰直角三角形，理由如下：
∵AB=AC，∠BAC=90°，
∴AD=DC．
∵△AFD∽△CGD，
∴
=
=1．
∴FD=DG．
∵∠FDG=90°，
∴△FDG为等腰直角三角形．（12分）
证明：（1）在△ADC和△EGC中，∵∠ADC=∠EGC，∠C=∠C，
∴△ADC∽△EGC．
∴
| EG |
| AD |
| CG |
| CD |
解：（2）FD与DG垂直．（4分）
证明如下：
在四边形AFEG中，
∵∠FAG=∠AFE=∠AGE=90°，
∴四边形AFEG为矩形．
∴AF=EG．
∵
| EG |
| AD |
| CG |
| CD |
∴
| AF |
| AD |
| CG |
| CD |
又∵△ABC为直角三角形，AD⊥BC，
∴∠FAD=∠C=90°-∠DAC，
∴△AFD∽△CGD．
∴∠ADF=∠CDG．（8分）
∵∠CDG+∠ADG=90°，
∴∠ADF+∠ADG=90°．
即∠FDG=90°．
∴FD⊥DG．（10分）
（3）当AB=AC时，△FDG为等腰直角三角形，理由如下：
∵AB=AC，∠BAC=90°，
∴AD=DC．
∵△AFD∽△CGD，
∴
| FD |
| GD |
| AD |
| DC |
∴FD=DG．
∵∠FDG=90°，
∴△FDG为等腰直角三角形．（12分）
点评：此题考查了相似三角形的判定和性质，①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；③如果两个三角形的两个对应角相等，那么这两个三角形相似．相似三角形的对应边的比相等，对应角相等．
练习册系列答案
相关题目
复数z=
（i为虚数单位），则|z|等于（ ）
| (2-i)(1+i) |
| i |
| A、10 | ||
B、
| ||
| C、5 | ||
D、
|