题目内容
函数f(x)=
sinωx•cosωx+sin2ωx+k,(ω>0).
(1)若f(x)图象中相邻两条对称轴间的距离不小于
,求ω的取值范围;
(2)若f(x)的最小正周期为π,且当x∈[-
,
]时,f(x)的最大值是
,求f(x)最小值,并说明如何由y=sin2x的图象变换得到y=f(x)的图象.
| 3 |
(1)若f(x)图象中相邻两条对称轴间的距离不小于
| π |
| 2 |
(2)若f(x)的最小正周期为π,且当x∈[-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
考点:二倍角的余弦,单位圆与周期性,两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用两角和与差的三角函数以及二倍角公式化简f(x)为一个角的一个三角函数的形式,通过图象中相邻两条对称轴间的距离不小于
,列出ω的不等式,即可求解ω的取值范围;
(2)利用f(x)的最小正周期为π,求出ω,当x∈[-
,
]时,求出相位的范围,通过f(x)的最大值是
,求出k,然后求解f(x)最小值,利用三角函数的平移变换说明由y=sin2x的图象变换得到y=f(x)的图象.
| π |
| 2 |
(2)利用f(x)的最小正周期为π,求出ω,当x∈[-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
解答:
(10分)
解:f(x)=
sin2ωx+
+k
=
sin2ωx-
cos2ωx+
+k
=sin(2ωx-
)+k+
.(3分)
(1)由题意可知
=
≥
,∴ω≤1.
又ω>0,∴0<ω≤1.(5分)
(2)∵T=
=π,∴ω=1.∴f(x)=sin(2x-
)+k+
.
∵x∈[-
,
],∴2x-
∈[-
,
]
从而当2x-
=
,即x=
时,fmax(x)=f(
)=sin
+k+
=k+1=
,
∴k=-
,故f(x)=sin(2x-
),
∴当2x-
=-
,即x=-
时f(x)取最小值-1(9分)
把y=sin2x的图象向右平移
个单位得到y=sin(2x-
)的图象. (10分)
解:f(x)=
| ||
| 2 |
| 1-cos2ωx |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2ωx-
| π |
| 6 |
| 1 |
| 2 |
(1)由题意可知
| T |
| 2 |
| π |
| 2ω |
| π |
| 2 |
又ω>0,∴0<ω≤1.(5分)
(2)∵T=
| π |
| ω |
| π |
| 6 |
| 1 |
| 2 |
∵x∈[-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
从而当2x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
∴k=-
| 1 |
| 2 |
| π |
| 6 |
∴当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
把y=sin2x的图象向右平移
| π |
| 12 |
| π |
| 6 |
点评:本题考查两角和与差的三角函数,二倍角公式的应用,三角函数的图象与性质,考查计算能力.

练习册系列答案
相关题目
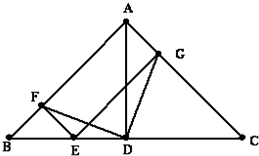 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为
如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为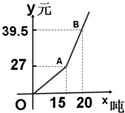 自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示. y=sinx+2|sinx|.
y=sinx+2|sinx|.