题目内容
已知α为锐角，且tan（
+α）=-2，计算
的值．
| π |
| 4 |
| 4sinα-2cosα |
| 5cosα+3sinα |
考点：同角三角函数基本关系的运用,两角和与差的正切函数
专题：三角函数的求值
分析：已知等式左边利用两角和与差的正切函数公式化简，整理求出tanα的值，原式分子分母除以cosα，利用同角三角函数间基本关系变形，将tanα的值代入计算即可求出值．
解答：
解：∵tan（
+α）=
，
∴
=-2，
整理得：1+tanα=-2+2tanα，即tanα=3，
∴cosα≠0，
则原式=
=
=
=
．
| π |
| 4 |
| 1+tanα |
| 1-tanα |
∴
| 1+tanα |
| 1-tanα |
整理得：1+tanα=-2+2tanα，即tanα=3，
∴cosα≠0，
则原式=
(4sinα-2cosα)×
| ||
(5cosα+3sinα)×
|
| 4tanα-2 |
| 5+3tanα |
| 4×3-2 |
| 5+3×3 |
| 5 |
| 7 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
若f（x）的定义域是[1，4]，那么f（x2）的定义域是（ ）
| A、[1，16] |
| B、[1，2] |
| C、[-2，-1] |
| D、[-2，-1]∪[1，2] |
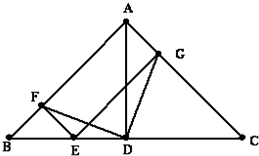如图，在△ABC中，∠BAC=90°，AD是BC边上的高，E是BC边上的一个动点（不与B，C重合），EF⊥AB，EG⊥AC，垂足分别为