题目内容
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C右焦点F(1,0),且e=
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B都不是顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
| 1 |
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B都不是顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆C右焦点F(1,0),且e=
,求出a,b,即可求椭圆C的标准方程;
(Ⅱ)直线l:y=kx+m与椭圆联立,利用以AB为直径的圆过椭圆的右顶点D(2,0),可得kADkBD=-1,即可得出结论.
| 1 |
| 2 |
(Ⅱ)直线l:y=kx+m与椭圆联立,利用以AB为直径的圆过椭圆的右顶点D(2,0),可得kADkBD=-1,即可得出结论.
解答:
解:(I)由题意设椭圆的标准方程为
+
=1(a>b>0),
由已知得:e=
且c=1,
∴a=2,∴b2=a2-c2=3.
∴椭圆的标准方程为
+
=1. …(4分)
(II)设A(x1,y1),B(x2,y2),
联立
得(3+4k2)x2+8mkx+4(m2-3)=0,
…(7分)
又y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2=
,…(8分)
因为以AB为直径的圆过椭圆的右顶点D(2,0),
∴kADkBD=-1,即
•
=-1,
∴y1y2+x1x2-2(x1+x2)+4=0,
∴
+
+
+4=0,
∴7m2+16mk+4k2=0.
解得:7m+2k=0或m+2k=0…(10分)
∴直线l过点(
,0)或点(2,0)(舍) …(12分)
| x2 |
| a2 |
| y2 |
| b2 |
由已知得:e=
| 1 |
| 2 |
∴a=2,∴b2=a2-c2=3.
∴椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(II)设A(x1,y1),B(x2,y2),
联立
|
|
又y1y2=(kx1+m)(kx2+m)=k2x1x2+mk(x1+x2)+m2=
| 3(m2-4k2) |
| 3+4k2 |
因为以AB为直径的圆过椭圆的右顶点D(2,0),
∴kADkBD=-1,即
| y1 |
| x1-2 |
| y2 |
| x2-2 |
∴y1y2+x1x2-2(x1+x2)+4=0,
∴
| 3(m2-4k2) |
| 3+4k2 |
| 4(m2-3) |
| 3+4k2 |
| 16mk |
| 3+4k2 |
∴7m2+16mk+4k2=0.
解得:7m+2k=0或m+2k=0…(10分)
∴直线l过点(
| 2 |
| 7 |
点评:本题考查圆锥曲线与方程.直线系过定点时,必需是直线系中的参数为但参数,对于含有双参数的直线系,就要找到两个参数之间的关系把直线系方程化为单参数的方程,然后把x,y当作参数的系数把这个方程进行整理,使这个方程关于参数无关的成立的条件就是一个关于x,y的方程组,以这个方程的解为坐标的点就是直线系过的定点.

练习册系列答案
相关题目
如图程序框图中,若输出S=
+
,则p的值为( )
| 3 |
| 2 |
| 3 |

| A、3 | B、4 | C、5 | D、6 |
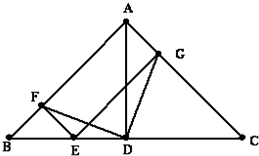 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为
如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为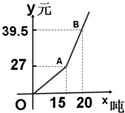 自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.