题目内容
已知直线l:
+
=1.
(1)若直线的斜率小于2,求实数m的取值范围;
(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最小值及此时直线的方程.
| x |
| m |
| y |
| 4-m |
(1)若直线的斜率小于2,求实数m的取值范围;
(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最小值及此时直线的方程.
考点:直线的一般式方程,直线的斜率
专题:直线与圆
分析:(1)利用斜率计算公式即可得出;
(2)求出与坐标轴的交点坐标,利用三角形的面积计算公式和二次函数的单调性即可得出.
(2)求出与坐标轴的交点坐标,利用三角形的面积计算公式和二次函数的单调性即可得出.
解答:
解:(1)直线l过点(m,0),(0,4-m),
则k=
<2,解得m>0或m<-4且m≠4.
∴实数m的取值范围是m>0或m<-4且m≠4;
(2)由m>0,4-m>0得0<m<4,
则S=
=
,
则m=2时,S有最大值,直线l的方程为x+y-2=0.
则k=
| 4-m |
| -m |
∴实数m的取值范围是m>0或m<-4且m≠4;
(2)由m>0,4-m>0得0<m<4,
则S=
| m(4-m) |
| 2 |
| -(m-2)2+4 |
| 2 |
则m=2时,S有最大值,直线l的方程为x+y-2=0.
点评:本题考查了斜率计算公式、三角形的面积计算公式和二次函数的单调性,考查了计算能力,属于基础题.

练习册系列答案
相关题目
把函数y=sinx(x∈R)的图象上所有的点向左平行移动
个单位长度,再将所得的图象的横坐标缩短到原来的
倍(纵坐标不变),得到的图象所表示的函数是( )
| π |
| 6 |
| 1 |
| 2 |
A、y=sin(
| ||||
B、y=sin(
| ||||
C、y=sin(2x+
| ||||
D、y=sin(2x+
|
圆C与圆(x+1)2+(y-2)2=1关于原点对称,则圆C的方程为( )
| A、(x-1)2+(y+2)2=1 |
| B、(x-1)2+(y-2)2=1 |
| C、(x-2)2+(y+1)2=1 |
| D、(x+1)2+(y-2)2=1 |
如图程序框图中,若输出S=
+
,则p的值为( )
| 3 |
| 2 |
| 3 |

| A、3 | B、4 | C、5 | D、6 |
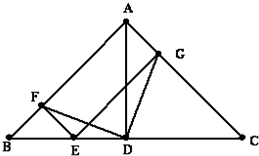 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为
如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为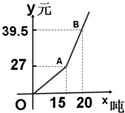 自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.