题目内容
已知数列{an}中,a1=1,an+1=
(n∈N*).
(1)求数列{an}的通项公式an;
(2)设
=
+1,求数列{bn•bn+1}的前n项和Tn.
(3)在(2)的条件下,求数列{
•2
}的前n项和Sn.
| an |
| 2an+1 |
(1)求数列{an}的通项公式an;
(2)设
| 2 |
| bn |
| 1 |
| an |
(3)在(2)的条件下,求数列{
| 1 |
| an |
| 1 |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)把数列递推式取倒数,得到数列{
}是以1为首项,以2为公差的等差数列,求出其通项公式后可得
数列{an}的通项公式an;
(2)把(1)中求出的通项公式代入
=
+1,整理后得到bn,代入数列{bn•bn+1}后利用裂项相消法求数列的和;
(3)把an,bn代入数列{
•2
},整理后利用错位相减法求数列{
•2
}的前n项和Sn.
| 1 |
| an |
数列{an}的通项公式an;
(2)把(1)中求出的通项公式代入
| 2 |
| bn |
| 1 |
| an |
(3)把an,bn代入数列{
| 1 |
| an |
| 1 |
| bn |
| 1 |
| an |
| 1 |
| bn |
解答:
解:(1)由an+1=
,得
-
=2,又
=1,
∴数列{
}是以1为首项,以2为公差的等差数列,
∴
=1+2(n-1)=2n-1,得an=
.
(2)由
=
+1,得
=2n-1+1=2n,∴bn=
,
从而bn•bn+1=
=
-
,
则Tn=b1b2+b2b3+…+bnbn+1=
+
+…+
=(
-
)+(
-
)+(
-
)+…+(
-
)
=1-
=
.
(3)由(1)(2)可知,
=2n-1,
=n
∴
•2
=(2n-1)•2n,
∴Sn=1•21+3•22+5•23+7•24+…+(2n-1)•2n,
∴2Sn=1•22+3•23+5•24+…+(2n-3)•2n+(2n-1)•2n+1,
两式作差得:
∴Sn=(2n-1)•2n+1+2-4•(2n-1).
| an |
| 2an+1 |
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| a1 |
∴数列{
| 1 |
| an |
∴
| 1 |
| an |
| 1 |
| 2n-1 |
(2)由
| 2 |
| bn |
| 1 |
| an |
| 2 |
| bn |
| 1 |
| n |
从而bn•bn+1=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则Tn=b1b2+b2b3+…+bnbn+1=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n+1) |
=(
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
(3)由(1)(2)可知,
| 1 |
| an |
| 1 |
| bn |
∴
| 1 |
| an |
| 1 |
| bn |
∴Sn=1•21+3•22+5•23+7•24+…+(2n-1)•2n,
∴2Sn=1•22+3•23+5•24+…+(2n-3)•2n+(2n-1)•2n+1,
两式作差得:
|
∴Sn=(2n-1)•2n+1+2-4•(2n-1).
点评:本题考查了数列递推式,考查了裂项相消法、错位相减法求数列的和,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆C与圆(x+1)2+(y-2)2=1关于原点对称,则圆C的方程为( )
| A、(x-1)2+(y+2)2=1 |
| B、(x-1)2+(y-2)2=1 |
| C、(x-2)2+(y+1)2=1 |
| D、(x+1)2+(y-2)2=1 |
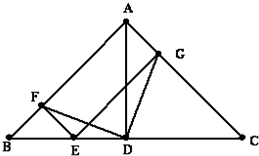 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为
如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为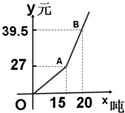 自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示.
自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若居民应交水费y(元)与用水量x(吨)的函数关系如图所示. y=sinx+2|sinx|.
y=sinx+2|sinx|.