题目内容
已知抛物线y2=4x,求以点P(2,-1)为中点的弦AB所在的直线方程.
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:设出弦AB所在的直线方程,与抛物线方程联立,设出A、B坐标,利用韦达定理,通过点P(2,-1)为中点,求出k的值,然后求出弦AB所在直线的方程.
解答:
解:设弦AB所在的直线方程为y-(-1)=k(x-2),即y=kx-2k-1.…(2分)
由
,消去x得ky2-4y-(8k+4)=0,①…(6分)
设A(x1,y1),B(x2,y2),所以y1+y2=
.…(8分)
因为P(2,-1)为弦AB中点,所以y1+y2=-2,
=-2,解得k=-2…(10分)
代入方程(1),验证△>0,合题意.
所以弦AB所在直线的方程为y=-2x+3,
即2x+y-3=0.…(12分)
由
|
设A(x1,y1),B(x2,y2),所以y1+y2=
| 4 |
| k |
因为P(2,-1)为弦AB中点,所以y1+y2=-2,
| 4 |
| k |
代入方程(1),验证△>0,合题意.
所以弦AB所在直线的方程为y=-2x+3,
即2x+y-3=0.…(12分)
点评:本题考查直线与抛物线的位置关系的应用,弦AB所在直线的方程的求法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
sin(-930°)的值是( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
如图程序框图中,若输出S=
+
,则p的值为( )
| 3 |
| 2 |
| 3 |

| A、3 | B、4 | C、5 | D、6 |
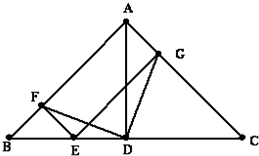 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为
如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为