题目内容
(1)已知0<x<
,求x(4-3x)的最大值;
(2)已知x,y都是正实数,且x+y-3xy+5=0,求xy的最小值.
| 4 |
| 3 |
(2)已知x,y都是正实数,且x+y-3xy+5=0,求xy的最小值.
考点:基本不等式
专题:不等式的解法及应用
分析:(1)把原式整理成
(3x)(4-3x)的形式,进而利用基本不等式求得其最大值.
(2)把原式转化为x+y+5=3xy,利用基本不等式得出关于
的一元二次不等式,进而求得
的范围,则xy的范围可得.
| 1 |
| 3 |
(2)把原式转化为x+y+5=3xy,利用基本不等式得出关于
| xy |
| xy |
解答:
解:(1)∵0<x<
,
∴x(4-3x)=
(3x)(4-3x)≤
(
)2=
,
当且仅当3x=4-3x,即x=
时等号成立,
∴x(4-3x)的最大值为
.
(2)由x+y-3xy+5=0,得x+y+5=3xy,
∴2
+5≤x+y+5=3xy,
∴3xy-2
-5≥0,
解得
≥
,即xy≥
,
∴xy的最小值为
.
| 4 |
| 3 |
∴x(4-3x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 3x+4-3x |
| 2 |
| 4 |
| 3 |
当且仅当3x=4-3x,即x=
| 2 |
| 3 |
∴x(4-3x)的最大值为
| 4 |
| 3 |
(2)由x+y-3xy+5=0,得x+y+5=3xy,
∴2
| xy |
∴3xy-2
| xy |
解得
| xy |
| 5 |
| 3 |
| 25 |
| 9 |
∴xy的最小值为
| 25 |
| 9 |
点评:本题主要考查了基本不等式的应用.注意三个条件的同时满足.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=
+
的最大值为M,最小值为m,则
的值为( )
| 1-x |
| x+5 |
| M |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
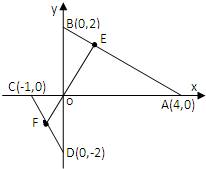 在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.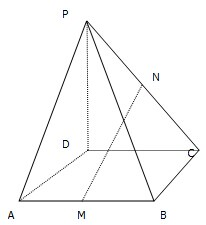 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.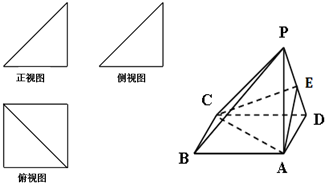 一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.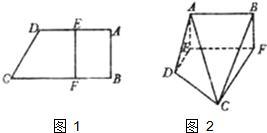 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.