题目内容
已知函数f(x)=ex-ax-1.
(1)求f(x)的单调增区间;
(2)是否存在a,使f(x)在(-2,3)上为减函数,若存在,求出a的取值范围,若不存在,说明理由.
(1)求f(x)的单调增区间;
(2)是否存在a,使f(x)在(-2,3)上为减函数,若存在,求出a的取值范围,若不存在,说明理由.
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)先求出函数的导数,再讨论①若a≤0,②若a>0的情况,从而求出单调区间;
(2)由f′(x)=ex-a≤0在(-2,3)上恒成立.从而a≥ex在x∈(-2,3)上恒成立,从而f(x)在(-2,3)上为减函数,得a≥e3.故存在实数a≥e3,使f(x)在(-2,3)上单调递减.
(2)由f′(x)=ex-a≤0在(-2,3)上恒成立.从而a≥ex在x∈(-2,3)上恒成立,从而f(x)在(-2,3)上为减函数,得a≥e3.故存在实数a≥e3,使f(x)在(-2,3)上单调递减.
解答:
解 f′(x)=ex-a,
(1)若a≤0,则f′(x)=ex-a≥0,
即f(x)在R上递增,
若a>0,ex-a≥0,∴ex≥a,x≥ln a.
因此f(x)的递增区间是[lna,+∞).
(2)由f′(x)=ex-a≤0在(-2,3)上恒成立.
∴a≥ex在x∈(-2,3)上恒成立.
又∵-2<x<3,∴e-2<ex<e3,只需a≥e3.
当a=e3时f′(x)=ex-e3在x∈(-2,3)上,f′(x)<0,
即f(x)在(-2,3)上为减函数,
∴a≥e3.
故存在实数a≥e3,使f(x)在(-2,3)上单调递减.
(1)若a≤0,则f′(x)=ex-a≥0,
即f(x)在R上递增,
若a>0,ex-a≥0,∴ex≥a,x≥ln a.
因此f(x)的递增区间是[lna,+∞).
(2)由f′(x)=ex-a≤0在(-2,3)上恒成立.
∴a≥ex在x∈(-2,3)上恒成立.
又∵-2<x<3,∴e-2<ex<e3,只需a≥e3.
当a=e3时f′(x)=ex-e3在x∈(-2,3)上,f′(x)<0,
即f(x)在(-2,3)上为减函数,
∴a≥e3.
故存在实数a≥e3,使f(x)在(-2,3)上单调递减.
点评:本题考察了函数的单调性,导数的应用,求参数的范围,是一道基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
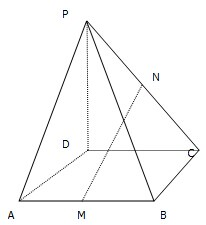 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.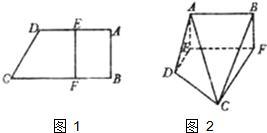 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.