题目内容
已知等差数列{an}中,a3=2,3a2+2a7=0,其前n项和为Sn.
(1)求等差数列{an}的通项公式;
(2)令bn=|
|,求数列{bn}的前n项和Tn.
(1)求等差数列{an}的通项公式;
(2)令bn=|
| Sn |
| n |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式求出首项和公差,由此能求出等差数列{an}的通项公式.
(2)Sn=7n-n2,
=7-n,设数列{
}的前n项和为Mn,当n≤7时,Tn=Mn;当n>7时,Tn=-Mn+2M7,由此能求出结果.
(2)Sn=7n-n2,
| Sn |
| n |
| Sn |
| n |
解答:
解:(1)∵等差数列{an}中,a3=2,3a2+2a7=0,
∴
,
解得a1=6,d=-2,
∴an=6+(n-1)×(-2)=8-2n.
(2)∵a1=6,d=-2,
∴Sn=6n+
×(-2)=7n-n2,
∴
=7-n,
∴{
}是首项为6,公差为-1的等差数列,
设数列{
}的前n项和为Mn,
则Mn=6n+
×(-1)=-
n2+
n,
当n≤7时,
Tn=Mn=6n+
×(-1)=-
n2+
n,n≤7.
当n>7时,Tn=-Mn+2M7=
n2-
n+42,n>7.
∴Tn=
.
∴
|
解得a1=6,d=-2,
∴an=6+(n-1)×(-2)=8-2n.
(2)∵a1=6,d=-2,
∴Sn=6n+
| n(n-1) |
| 2 |
∴
| Sn |
| n |
∴{
| Sn |
| n |
设数列{
| Sn |
| n |
则Mn=6n+
| n(n-1) |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
当n≤7时,
Tn=Mn=6n+
| n(n-1) |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
当n>7时,Tn=-Mn+2M7=
| 1 |
| 2 |
| 13 |
| 2 |
∴Tn=
|
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
命题“若∠C=90°,则△ABC是直角三角形”它的逆命题是( )命题.
| A、真 | B、假 | C、不确定 | D、D、 |
正三棱锥底面边长为3,侧棱与底面成60°角,则正三棱锥外接球面积为( )
| A、4π | ||
B、4
| ||
| C、16π | ||
D、16
|
已知向量
,
满足|
|=3,且|
+
|=|
-
|=5,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
已知函数y=
+
的最大值为M,最小值为m,则
的值为( )
| 1-x |
| x+5 |
| M |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
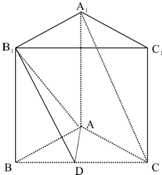 如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.
如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.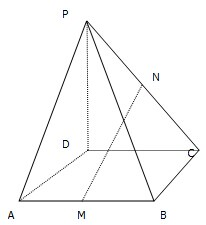 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.