题目内容
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=-
(1)求x<0时,f(x)的解析式;
(2)求f(x)的值域.
| 7x |
| x2+x+1 |
(1)求x<0时,f(x)的解析式;
(2)求f(x)的值域.
考点:函数奇偶性的性质,函数的值域,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)首先求出f(-x)的解析式,然后根据函数f(x)是定义在R上的偶函数,可得函数f(x)=f(-x),据此解答即可;
(2)分类求出f(x)的值域,x=0时,y=0;首先变形:x>0时,f(x)=-
=-
,然后根据x+
≥2,求出x>0时,f(x)的取值范围是多少;最后根据f(x)是定义在R上的偶函数,求出x<0时,f(x)的取值范围是多少,据此解答即可.
(2)分类求出f(x)的值域,x=0时,y=0;首先变形:x>0时,f(x)=-
| 7x |
| x2+x+1 |
| 7 | ||
x+
|
| 1 |
| x |
解答:
解:(1)令x<0,则-x>0,
所以f(-x)=-
=
因为y=f(x)是定义在R上的偶函数,
所以f(-x)=f(x),
所以x<0时,f(x)=
(2)①x=0时,y=0
②x>0时,f(x)=-
=-
因为x+
≥2,所以x+
+1≥3
所以0<
≤
,-
≤-
<0
即x>0时,-
≤y<0
③因为y=f(x)是定义在R上的偶函数,
所以x<0时,-
≤y<0
综上,f(x)的值域是[-
,0].
所以f(-x)=-
| 7(-x) |
| x2-x+1 |
| 7x |
| x2-x+1 |
因为y=f(x)是定义在R上的偶函数,
所以f(-x)=f(x),
所以x<0时,f(x)=
| 7x |
| x2-x+1 |
(2)①x=0时,y=0
②x>0时,f(x)=-
| 7x |
| x2+x+1 |
| 7 | ||
x+
|
因为x+
| 1 |
| x |
| 1 |
| x |
所以0<
| 7 | ||
x+
|
| 7 |
| 3 |
| 7 |
| 3 |
| 7 | ||
x+
|
即x>0时,-
| 7 |
| 3 |
③因为y=f(x)是定义在R上的偶函数,
所以x<0时,-
| 7 |
| 3 |
综上,f(x)的值域是[-
| 7 |
| 3 |
点评:本题主要考查了函数的解析式的求法,以及函数的值域的求法.

练习册系列答案
相关题目
已知向量
,
满足|
|=3,且|
+
|=|
-
|=5,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
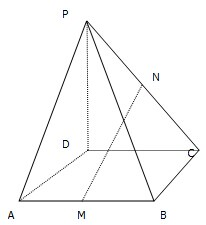 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.