题目内容
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=2| 2 |
(1)证明AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P-BD-A的平面角的正切值.
考点:二面角的平面角及求法,异面直线及其所成的角,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由勾股定理逆定理,结合题中的数据得到AD⊥PA,又AD⊥AB,PA、AB是平面PAB内的相交直线,所以AD⊥平面PAB;
(2)利用条件借助图形,利用异面直线所成角的定义找到共面的两条相交直线,然后结合解三角形有关知识解出即可;
(3)通过把二面角转化为其平面角PEH,然后在RT△PHE中,求出其正切值即可.
(2)利用条件借助图形,利用异面直线所成角的定义找到共面的两条相交直线,然后结合解三角形有关知识解出即可;
(3)通过把二面角转化为其平面角PEH,然后在RT△PHE中,求出其正切值即可.
解答:
(1)证明:在△PAD中,由题设PA=AD=2,PD=2
,可得PA2+AD2=PD2,于是AD⊥PA,
∵在矩形ABCD中,AD⊥AB,PA、AB是平面PAB内的相交直线,
∴AD⊥平面PAB;
(2)解:由题设,BC∥AD,
∴∠PCB(或其补角)是异面直线PC与AD所成的角.
在△PAB中,由余弦定理得PB=
=2
由(1)知AD⊥平面PAB,PB?平面PAB,
∴AD⊥PB,因而BC⊥PB,于是△PBC是直角三角形,故tanPCB=
.
∴异面直线PC与AD所成的角的大小为60°.
(3)解:过点P做PH⊥AB于H,
过点H做HE⊥BD于E,连接PE
∵AD⊥平面PAB,PH?平面PAB,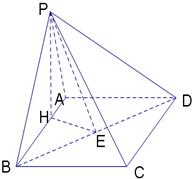
∞AD⊥PH.
又AD∩AB=A,
因而PH⊥平面ABCD,故HE为PE在平面ABCD内的射影.
∴BD⊥PE,
从而∠PEH是二面角P-BD-A的平面角.
由题设可得,PH=PA•sin60°=
,AH=PA•cos60°=1,BH=AB-AH=3,
BD=2
,HE=
•BH=
,
于是在RT△PHE中,tan∠PEH=
=
,
∴二面角P-BD-A的正切值大小为
.
| 2 |
∵在矩形ABCD中,AD⊥AB,PA、AB是平面PAB内的相交直线,
∴AD⊥平面PAB;
(2)解:由题设,BC∥AD,
∴∠PCB(或其补角)是异面直线PC与AD所成的角.
在△PAB中,由余弦定理得PB=
4+16-2•2•4•
|
| 3 |
由(1)知AD⊥平面PAB,PB?平面PAB,
∴AD⊥PB,因而BC⊥PB,于是△PBC是直角三角形,故tanPCB=
| 3 |
∴异面直线PC与AD所成的角的大小为60°.
(3)解:过点P做PH⊥AB于H,
过点H做HE⊥BD于E,连接PE
∵AD⊥平面PAB,PH?平面PAB,

∞AD⊥PH.
又AD∩AB=A,
因而PH⊥平面ABCD,故HE为PE在平面ABCD内的射影.
∴BD⊥PE,
从而∠PEH是二面角P-BD-A的平面角.
由题设可得,PH=PA•sin60°=
| 3 |
BD=2
| 5 |
| AD |
| BD |
| 3 | ||
|
于是在RT△PHE中,tan∠PEH=
| ||||
|
| ||
| 3 |
∴二面角P-BD-A的正切值大小为
| ||
| 3 |
点评:本题考查线面垂直的判定,以及二面角的证明,通过对四棱锥的考查,以及直角三角形的考查,得到要求的结果,属于中档题.

练习册系列答案
相关题目
正三棱锥的高是
,侧棱长为
,那么侧面与底面所成的二面角是( )
| 3 |
| 7 |
| A、60° | B、30° |
| C、45° | D、75° |
如图所示是函数f(x)的导函数f′(x)的图象,则下列判断中正确的是( )


| A、函数f(x)在区间(-2,0)上是减函数 |
| B、函数f(x)在区间(1,3)上是减函数 |
| C、函数f(x)在区间(0,2)上是减函数 |
| D、函数f(x)在区间(3,4)上是增函数 |
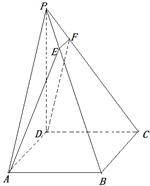 如图,已知ABCD是正方形,PD⊥平面ABCD,
如图,已知ABCD是正方形,PD⊥平面ABCD,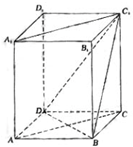 如图,四棱柱ABCD-A1B1C1D1的底面是正方形,且侧棱和底面垂直.
如图,四棱柱ABCD-A1B1C1D1的底面是正方形,且侧棱和底面垂直. 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.