题目内容
若二项式(
+
)5的展开式中的第四项的值是
,则实数x的值为 .
| x |
| 1 |
| 2 |
| 5 |
| 2 |
考点:二项式定理的应用
专题:计算题,二项式定理
分析:运用二项式展开式的通项公式求出通项,再令r=3,解方程,即可得到x.
解答:
解:二项式(
+
)5的展开式的通项公式为
Tr+1=
(
)5-r(
)r,
由于展开式中的第四项的值是
,
则
(
)2(
)3=
,
即10x=20,
解得x=2.
故答案为:2.
| x |
| 1 |
| 2 |
Tr+1=
| C | r 5 |
| x |
| 1 |
| 2 |
由于展开式中的第四项的值是
| 5 |
| 2 |
则
| C | 3 5 |
| x |
| 1 |
| 2 |
| 5 |
| 2 |
即10x=20,
解得x=2.
故答案为:2.
点评:本题考查二项式的展开式的通项公式的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
若直线y=x+b与圆(x-1)2+y2=1有两个不同的公共点,则实数b的取值范围为( )
A、(-
| ||||
B、(-∞,
| ||||
C、(-∞,-
| ||||
D、[-
|
6个同学任意选3个参加一个会议,共有选法种数( )种.
| A、15 | B、10 | C、60 | D、20 |
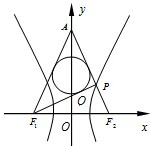 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
已知0为坐标原点,向量
=(1,3),
=(3,-1)且
=2
,则点P的坐标为( )
| OA |
| OB |
| AP |
| PB |
| A、(2,-4) | ||||
B、(
| ||||
C、(
| ||||
| D、(-2,4) |