题目内容
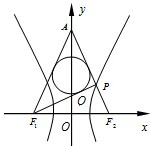如图，已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
考点：双曲线的简单性质
专题：
分析：本题先根据直角三角形内切圆半径得到边长的关系，结合双曲线定义和图形的对称必，求出a的值，由|F1F2|=6求出c的值，从而得到双曲线的离心率，得到本题结论．
解答：
解：∵PF1⊥PF2，△APF1的内切圆半径为
，
∴|PF1|+|PA|-|AF1|=2
，
∴|PF2|+2a+|PA|-|AF1|=2
，
∴|AF2|-|AF1|=2
-2a，
∵由图形的对称性知：|AF2|=|AF1|，
∴a=
．
∵，|F1F2|=6，
∴c=3，
∴e=
=
=
．
故选D．
| 3 |
∴|PF1|+|PA|-|AF1|=2
| 3 |
∴|PF2|+2a+|PA|-|AF1|=2
| 3 |
∴|AF2|-|AF1|=2
| 3 |
∵由图形的对称性知：|AF2|=|AF1|，
∴a=
| 3 |
∵，|F1F2|=6，
∴c=3，
∴e=
| c |
| a |
| 3 | ||
|
| 3 |
故选D．
点评：本题考查了双曲线的定义、图形的对称性，本题难度不大，属于基础题．
练习册系列答案
相关题目
设奇函数f（x）在（0，+∞）上为单调递减函数，且f（2）=0，则不等式f（x）＜0的解集为（ ）
| A、（-∞，-2）∪（0，2） |
| B、（-∞，-2）∪（2，+∞） |
| C、（-2，0）∪（2，+∞） |
| D、（-2，0）∪（0，2） |