题目内容
已知0为坐标原点，向量
=（1，3），
=（3，-1）且
=2
，则点P的坐标为（ ）
| OA |
| OB |
| AP |
| PB |
| A、（2，-4） | ||||
B、（
| ||||
C、（
| ||||
| D、（-2，4） |
考点：平行向量与共线向量
专题：平面向量及应用
分析：设出点P的坐标，表示出
、
，根据题意列出方程组，求出P点的坐标．
| AP |
| PB |
解答：
解：设点P（x，y），根据题意得；
=（x-1，y-3），
=（3-x，-1-y）；
∵
=2
，
∴
，
解得x=
，y=
；
∴P（
，
）．
故选：C．
| AP |
| PB |
∵
| AP |
| PB |
∴
|
解得x=
| 7 |
| 3 |
| 1 |
| 3 |
∴P（
| 7 |
| 3 |
| 1 |
| 3 |
故选：C．
点评：本题考查了平面向量的坐标表示与运算的应用问题，解题时应设出点P的坐标，利用方程组求出答案，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
在复平面内，复数
对应的点的坐标为（ ）
| 13i |
| 3+2i |
| A、（3，2） |
| B、（3，-2） |
| C、（2，3） |
| D、（-2，3） |
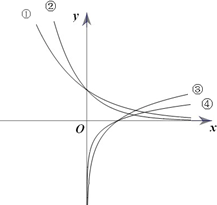如图，设实数a，b，c，d＞0，且不等于1，曲线①，②，③，④分别表示函数y=ax，y=bx，y=logcx，y=logdx在同一坐标系中的图象，则a，b，c，d的大小顺序为