题目内容
已知A（-3，1），B（3，1），C（1，3），则△ABC中BC边上的高所在的直线方程为（ ）
| A、x+y=0 |
| B、x-y+4=0 |
| C、x+y+2=0 |
| D、x-y=0 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：利用斜率坐标公式求出直线AB的斜率，再根据垂直关系求出AB边上的高线的斜率，然后根据点斜式方程求直线方程即可．
解答：
解：KBC=
=-1，∴BC边上的高线的斜率K=1，
∴BC边上的高线的点斜式方程为：y-1=x+3，即x-y+4=0．
故选：B．
| 1-3 |
| 3-1 |
∴BC边上的高线的点斜式方程为：y-1=x+3，即x-y+4=0．
故选：B．
点评：本题考查直线的斜率坐标公式、直线的点斜式方程及直线垂直的条件．两条直线垂直（斜率存在且不为0），其斜率之积为-1．
练习册系列答案
相关题目
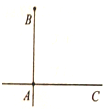如图，两高速公路线垂直相交于站A，若已知AB=100千米，甲汽车从A站出发，沿AC方向以50千米/小时的速度行驶，同时乙汽车从B站出发，一年BA方向以v千米/小时的速度行驶，至A站即停止前行（甲车仍继续行驶）（两车的车长忽略不计）．