题目内容
已知f(x)是定义在R上的函数,且满足f(x+2)[1-f(x)]=1+f(x),f(1)=2,则f(2017)= .
考点:函数的值
专题:计算题,函数的性质及应用
分析:由f(x+2)[1-f(x)]=1+f(x)可推出f(x+4)=-
,进而推出f(x+8)=f(x),从而解得.
| 1 |
| f(x) |
解答:
解:∵f(x+2)[1-f(x)]=1+f(x),
∴f(x+2)=
;
∴f(x+4)=
=
=-
;
∴f(x+8)=-
=f(x);
故f(2017)=f(252×8+1)=f(1)=2;
故答案为:2.
∴f(x+2)=
| 1+f(x) |
| 1-f(x) |
∴f(x+4)=
| 1+f(x+2) |
| 1-f(x+2) |
=
1+
| ||
1-
|
| 1 |
| f(x) |
∴f(x+8)=-
| 1 |
| f(x+4) |
故f(2017)=f(252×8+1)=f(1)=2;
故答案为:2.
点评:本题考查了函数的性质的判断与应用,属于基础题.

练习册系列答案
相关题目
已知A(-3,1),B(3,1),C(1,3),则△ABC中BC边上的高所在的直线方程为( )
| A、x+y=0 |
| B、x-y+4=0 |
| C、x+y+2=0 |
| D、x-y=0 |
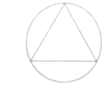 某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )
某人随机地向如图所示的正三角形及其外接圆区域内部设计(不包括三角形及其外接圆的边界),则针孔到正三角形内部(不包括边界)的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|