题目内容
16.已知幂函数y=f(x)的图象过点(2,4),则log2f($\frac{1}{2}$)=( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
分析 设出幂函数的解析式,求出函数的解析式,计算log2f($\frac{1}{2}$)的值即可.
解答 解:设幂函数y=f(x)=xα,
其图象过点(2,4),
∴2α=4,
解得α=2;
∴f(x)=x2,
∴f($\frac{1}{2}$)=$\frac{1}{4}$,
∴log2f($\frac{1}{2}$)=log2$\frac{1}{4}$=-2,
故选:D.
点评 本题考查了求函数的解析式问题,考查幂函数的定义以及对数函数的运算,是一道基础题.

练习册系列答案
相关题目
6.在平面直角坐标系xOy中,不等式组$\left\{\begin{array}{l}{(x-y-1)(x+y-1)≥0}\\{-1≤x≤3}\end{array}\right.$表示的平面区域的面积为( )
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
7.某车间加工零件的数量x与加工时间y的统计数据如表:
现已求得如表数据的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为102分钟.
| 零件数x(个) | 18 | 20 | 22 |
| 加工时间y(分钟) | 27 | 30 | 33 |
4.函数f(x)是定义在R上的奇函数,对任意两个不相等的正数x1,x2,都有$\frac{{x}_{2}f({x}_{1})-{x}_{1}f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,记a=-log23•f(log${\;}_{\frac{1}{3}}$2),b=f(1),c=4f(0.52),则( )
| A. | c<b<a | B. | b<a<c | C. | c<a<b | D. | a<b<c |
8.直线x-y-1=0的倾斜角与其在y轴上的截距分别是( )
| A. | 135°,1 | B. | 45°,-1 | C. | 45°,1 | D. | 135°,-1 |
13.已知函数f(x)=Asin(ωx+φ)+B,(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,则( )
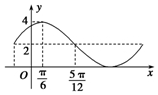

| A. | A=4 | B. | ω=1 | C. | φ=$\frac{π}{6}$ | D. | B=4 |
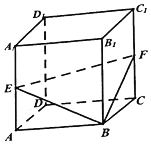 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱AA1,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面BEF,则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$,$\sqrt{2}$].