题目内容
6.mn>0是$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1表示椭圆的( )条件.| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
分析 mn>0时,$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1不一定表示椭圆,$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1表示椭圆⇒当m,n都是正数且m≠n⇒mn>0.
解答 解:mn>0,当m,n都是正数且m≠n时,$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1表示椭圆,
$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1表示椭圆⇒当m,n都是正数且m≠n⇒mn>0.
∴mn>0是$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1表示椭圆的必要不充分条件.
故选:B.
点评 本题考查充分不必要条件、必要不充分条件、充要条件、不充分不必要条件的判断,是基础题,解题时要认真审题,注意椭圆的性质的合理运用.

练习册系列答案
相关题目
16.已知$|{\overrightarrow{AB}}|=|{\overrightarrow{AC}}|=2,\overrightarrow{AB}•\overrightarrow{AC}=2\sqrt{3}$,平面区域D由所有满足$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$(1≤λ≤a,1≤μ≤b)的点P构成,其面积为8,则4a+b的最小值为( )
| A. | 13 | B. | 12 | C. | $7\sqrt{2}$ | D. | $6\sqrt{2}$ |
14.某产品的广告费x(万元)与销售额y(万元)的统计数据如表:
根据如表可知回归直线方程$\stackrel{∧}{y}$=7x+$\stackrel{∧}{a}$,若广告费用为10万元,则预计销售额为73.5万元.
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
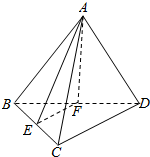 如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.
如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$. 如图,在三棱柱ABC-A1B1C1中,AA1=A1C,D,E,F分别为AB,A1C1,AA1的中点,平面AA1C1C⊥平面ABC.G,H分别在AD,AC上,且AD=4AG,GH∥CD.求证:
如图,在三棱柱ABC-A1B1C1中,AA1=A1C,D,E,F分别为AB,A1C1,AA1的中点,平面AA1C1C⊥平面ABC.G,H分别在AD,AC上,且AD=4AG,GH∥CD.求证: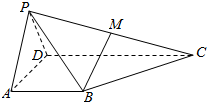 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD,AB⊥AD,AB∥CD,点M是PC的中点.