题目内容
3.计算下列各式的值(1)$({-2{x^{\frac{1}{4}}}{y^-}^{\frac{1}{3}}})({3{x^{-\frac{1}{2}}}{y^{\frac{2}{3}}}})({-4{x^{\frac{1}{4}}}{y^{\frac{2}{3}}}})$;
(2)(log43+log83)(log32+log92).
分析 (1)利用有理指数幂的有身份证化简求解即可.
(2)利用对数运算法则化简求解即可.
解答 解:(1)$({-2{x^{\frac{1}{4}}}{y^-}^{\frac{1}{3}}})({3{x^{-\frac{1}{2}}}{y^{\frac{2}{3}}}})({-4{x^{\frac{1}{4}}}{y^{\frac{2}{3}}}})$=[-2×3×(-4)]${x}^{\frac{1}{4}-\frac{1}{2}+\frac{1}{4}}$${y}^{-\frac{1}{3}+\frac{2}{3}+\frac{2}{3}}$=24y;
(2)(log43+log83)(log32+log92)=($\frac{1}{2}$log23+$\frac{1}{3}$log23)(log32+$\frac{1}{2}$log32)=$\frac{5}{6}×\frac{3}{2}$=$\frac{5}{4}$.
点评 本题考查有理指数幂以及对数运算法则的应用,考查计算能力.

练习册系列答案
相关题目
13.焦点在x轴,且焦点到准线的距离为4的抛物线方程为( )
| A. | y2=4x | B. | y2=8x | C. | y2=±4x | D. | y2=±8x |
14.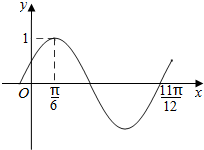 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
18.设等差数列{an}满足a3=5,a10=-9.则{an}的前n项和Sn取得最大值是( )
| A. | 23 | B. | 25 | C. | 27 | D. | 29 |
8.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
已知在这30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
参考数据:
参考公式:K2=$\frac{n(ad-cb)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整.
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
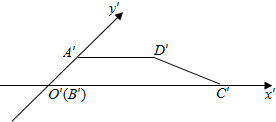 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是2$\sqrt{2}$.