题目内容
已知F1，F2为椭圆
+
=1的两个焦点，过F1的直线交椭圆于A，B两点，|AB|=8，则|AF2|+|BF2|=（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| A、2 | B、10 | C、12 | D、14 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据已知条件，由椭圆定义知：|AB|+|AF2|+|BF2|=4a，由此能求出结果．
解答：
解：椭圆
+
=1中，a=5，
∵F1，F2为椭圆
+
=1的两个焦点，过F1的直线交椭圆于A，B两点，
∴由椭圆定义知：|AB|+|AF2|+|BF2|=4a=20，
∵|AB|=8，
∴|AF2|+|BF2|=20-8=12．
故选：C．
| x2 |
| 25 |
| y2 |
| 9 |
∵F1，F2为椭圆
| x2 |
| 25 |
| y2 |
| 9 |
∴由椭圆定义知：|AB|+|AF2|+|BF2|=4a=20，
∵|AB|=8，
∴|AF2|+|BF2|=20-8=12．
故选：C．
点评：本题考查两条线段和的求法，是基础题，解题时要认真审题，要熟练掌握椭圆的简单性质．
练习册系列答案
相关题目
已知点G是△ABC的重心，若∠A=120°，
•
=-2，则|
|的最小值是（ ）
| AB |
| AC |
| AG |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
“x＜-2”是“x≤0”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
如果两个球的体积之比为1：8，那么两个球的表面积之比为（ ）
| A、8：27 | B、1：2 |
| C、1：4 | D、1：8 |
“0＜x＜2”是“x2-x＜0”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
在（-π，2π）内与
终边相同的角有（ ）个．
| 3π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
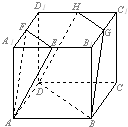如图，E，F，G，H分别为正方体AC1的棱A1B1，A1D1，B1C1，D1C1的中点，