题目内容
函数y=1-
sinx的单调区间是( )
| 2 |
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:根据复合函数单调性之间的关系以及正弦函数的单调性即可得到结论.
解答:
解:当sinx单调递增时,函数y=1-
sinx单调递减,
当sinx单调递减时,函数y=1-
sinx单调递增,
即当x∈[-
+2kπ,
+2kπ]时,y=sinx单调递增,
此时函数y=1-
sinx的单调递减,
故选:B.
| 2 |
| 3 |
当sinx单调递减时,函数y=1-
| 2 |
| 3 |
即当x∈[-
| π |
| 2 |
| π |
| 2 |
此时函数y=1-
| 2 |
| 3 |
故选:B.
点评:本题主要考查函数单调性的判断,利用复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
“x<-2”是“x≤0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
“0<x<2”是“x2-x<0”的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
如果执行如图的框图,输入N=5,则输出的数等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
在(-π,2π)内与
终边相同的角有( )个.
| 3π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
已知方程组
对此方程组的每一组正实数解(x,y,z,u),其中z≥y,都存在正实数M,且满足M≤
,则M的最大值是( )
|
| z |
| y |
| A、1 | ||
B、3+2
| ||
C、6+4
| ||
D、3-2
|
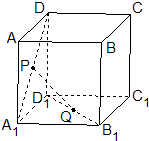 正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.
正方体ABCD-A1B1C1D1的棱长为1,P、Q分别是正方形AA1D1D和A1B1C1D1的中心.