题目内容
6.已知圆柱的底面半径为4,用与圆柱底面成30°角的平面截这个圆柱得到一个椭圆,建立适当的坐标系,求该椭圆的标准方程和离心率.分析 根据圆柱的直径算出椭圆的短轴长,再由二面角的平面角等于30°,利用三角函数定义可算出椭圆的长轴.由此求截面椭圆的方程,进一步求出椭圆的离心率.
解答 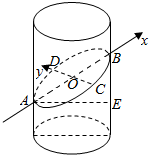 解:∵圆柱的底面半径为4,∴椭圆的短轴2b=8,得b=4,
解:∵圆柱的底面半径为4,∴椭圆的短轴2b=8,得b=4,
又∵椭圆所在平面与圆柱底面所成角为30°,
∴cos30°=$\frac{8}{2a}$,得$a=\frac{8\sqrt{3}}{3}$.
以AB所在直线为x轴,以AB的中垂线为y轴建立平面直角坐标系,
则椭圆方程为:$\frac{{x}^{2}}{\frac{64}{3}}+\frac{{y}^{2}}{16}=1$.
${c}^{2}={a}^{2}-{b}^{2}=\frac{64}{3}-16=\frac{16}{3}$,∴$c=\frac{4\sqrt{3}}{3}$.
∴椭圆的离心率为:e=$\frac{c}{a}=\frac{\frac{4\sqrt{3}}{3}}{\frac{8\sqrt{3}}{3}}=\frac{1}{2}$.
点评 本题以一个平面截圆柱,求载得椭圆的焦距,着重考查了平面与平面所成角的含义和椭圆的简单几何性质等知识,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
12.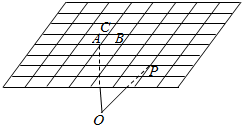 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )| A. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B. | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C. | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |
18.一个椭圆的半焦距为2,离心率e=$\frac{2}{3}$,则它的短轴长是( )
| A. | 3 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 6 |
15.如图,正方体中,两条异面直线BC1与B1D1所成的角是( )
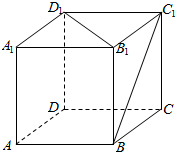

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |