题目内容
14.从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上一点M向x轴作垂线,垂足恰为左焦点F1,点A、B是椭圆与x轴正半轴、y轴正半轴的交点,且AB∥OM,|F1A|=$\sqrt{10}+\sqrt{5}$.(Ⅰ)求该椭圆的离心率;
(Ⅱ) 若P是该椭圆上的动点,右焦点为F2,求$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的取值范围.
分析 (Ⅰ)先计算PF1的长,再利用两直线平行得tan∠MOF1,最后在直角三角形MOF1中,找到a、b、c间的等式,从而求出离心率;
(Ⅱ)由|F1A|=$\sqrt{10}+\sqrt{5}$,可得a+c=$\sqrt{10}+\sqrt{5}$,再由a=$\sqrt{2}$c,解得a,c,再求b,进而得到椭圆方程,设出P的坐标,运用向量的数量积的坐标表示,结合椭圆的范围,即可得到所求的最值,进而得到所求范围.
解答 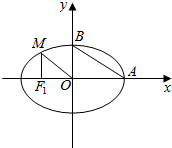 解:(Ⅰ)设F1(-c,0),
解:(Ⅰ)设F1(-c,0),
将x=-c代入椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),
得y=±$\frac{{b}^{2}}{a}$,
∴|PF1|=$\frac{{b}^{2}}{a}$,|OF1|=c,
∵AB∥OM,∴tan∠POF1=tan∠BAO=$\frac{b}{a}$,
∴在直角三角形MOF1中,tan∠MOF1=$\frac{|M{F}_{1}|}{|O{F}_{1}|}$=$\frac{{b}^{2}}{ac}$=$\frac{b}{a}$,
∴b=c,∴a=$\sqrt{2}$c,
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
(Ⅱ) 由|F1A|=$\sqrt{10}+\sqrt{5}$,
可得a+c=$\sqrt{10}+\sqrt{5}$,
又a=$\sqrt{2}$c,解得a=$\sqrt{10}$,c=$\sqrt{5}$,b=$\sqrt{5}$,
则椭圆的方程为$\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{5}$=1.
设P(m,n),可得m2+2n2=10,
又F1(-$\sqrt{5}$,0),F2($\sqrt{5}$,0),
$\overrightarrow{P{F}_{1}}$=(-$\sqrt{5}$-m,-n),$\overrightarrow{P{F}_{2}}$=($\sqrt{5}$-m,-n),
即有$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=(-$\sqrt{5}$-m)($\sqrt{5}$-n)+n2
=m2+n2-5=10-n2-5=5-n2,
由-$\sqrt{5}$≤n≤$\sqrt{5}$,
可得n=0,取得最大值5,n=$\sqrt{5}$时,取得最小值0.
则$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的取值范围是[0,5].
点评 本题考查椭圆的方程和性质,考查椭圆离心率的求法,注意运用两直线平行的条件,考查平面向量的数量积的范围,注意运用坐标表示,结合椭圆的范围,属于中档题.

| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
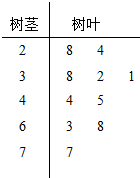 我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
我国政府对PM2.5采用如下标准:某市环保局从一年365天的市区PM2.5监测数据中,随机抽取10天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).| PM2.5日均值m(微克/立方米) | 空气质量等级 |
| m<35 | 一级 |
| 35≤m≤75 | 二级 |
| m>75 | 超标 |
(2)从这10天数据中任取4天的数据,记ξ为空气质量达到一级的天数,求ξ的分布列和期望;
(3)以这10天的数据来估计这一年365天的空气质量情况,并假定每天之间的空气质量相互不影响.记η为这一年中空气质量达到一级的天数,求η的平均值.