题目内容
1．椭圆4x2+9y2=144内有一点P（3，2），过P点的弦恰好以P点为中点，则求此弦所在的直线方程．分析 设所求直线与椭圆相交的两点的坐标，然后利用点差法求得直线的斜率，最后代入直线方程的点斜式得答案．
解答 解：设弦的端点为A（x1，y1），B（x2，y2），
则x1+x2=6，y1+y2=4，
把A、B坐标代入椭圆方程得，4x12+9y12=144，4x22+9y22=144，
两式相减得，4（x12-x22）+9（y12-y22）=0，即4（x1+x2）（x1-x2）+9（y1+y2）（y1-y2）=0，
所以kAB=-$\frac{2}{3}$，
所以这弦所在直线方程为：y-2=-$\frac{2}{3}$（x-3），即2x+3y-12=0．
点评 本题考查了直线与圆锥曲线的关系，训练了点差法求与中点弦有关的问题，是中档题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
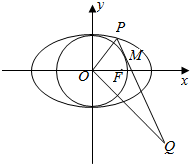在平面直角坐标系xOy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，右焦点F（1，0），点P在椭圆C上，且在第一象限内，直线PQ与圆O：x2+y2=b2相切于点M．
如图，椭圆M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，直线x=±a和y=±b所围成的矩形ABCD的面积为32$\sqrt{3}$．