题目内容
12.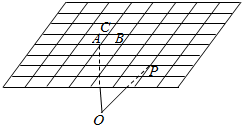 如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )
如图所示,已知A,B,C三点不共线,P为一定点,O为平面ABC外任意一点,则下列能表示向量$\overrightarrow{OP}$的为( )| A. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$+2$\overrightarrow{AC}$ | B. | $\overrightarrow{OA}$-3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | C. | $\overrightarrow{OA}$+3$\overrightarrow{AB}$-2$\overrightarrow{AC}$ | D. | $\overrightarrow{OA}$+2$\overrightarrow{AB}$-3$\overrightarrow{AC}$ |
分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AP}$,则$\overrightarrow{OP}$=$\overrightarrow{AP}-\overrightarrow{AO}$.
解答 解:以AP为对角线,以AB,AC所在直线为邻边做平行四边形,则$\overrightarrow{AP}$=3$\overrightarrow{AB}-2\overrightarrow{AC}$,
∴$\overrightarrow{OP}$=$\overrightarrow{AP}-\overrightarrow{AO}$=3$\overrightarrow{AB}-2\overrightarrow{AC}$+$\overrightarrow{OA}$,
故选:C.
点评 本题考查了空间向量的加减运算,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.函数y=$\frac{ln(x+1)}{{\sqrt{{3^x}-27}}}$的定义域为( )
| A. | (-1,+∞) | B. | (-1,3) | C. | (3,+∞) | D. | [3,+∞) |
3.空间四边形ABCD中,M、G分别是BC、CD的中点,则$\overrightarrow{MG}$-$\overrightarrow{AB}$+$\overrightarrow{AD}$等于( )
| A. | $\frac{3}{2}$$\overrightarrow{DB}$ | B. | 3$\overrightarrow{MG}$ | C. | 3$\overrightarrow{GM}$ | D. | 2$\overrightarrow{MG}$ |
4.若圆锥的底面与顶点都在球O的球面上,且圆锥的底面半径为1,体积为π,则球O的表面积为( )
| A. | $\frac{16π}{9}$ | B. | $\frac{100π}{9}$ | C. | 25π | D. | 36π |
1.对于每一个实数x,设f(x)是4x+1,x+2和4-2x三个函数中的最小值,则f(x)的最大值是( )
| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |