题目内容

已知△ABC是边长为1的正三角形，将BC边n等分，沿从B到C的方向的分点依次为P1、P2、P3、…、Pn-1，设Sn=
AB
•
AP1
+
AP1
•
AP2
+
AP2
•
AP3
…+
APn-1
•
AC
，求证：Sn=
5n2-2
6n
（n∈N+，n≥2）．
考点：数列的求和,平面向量数量积的运算
专题：等差数列与等比数列,平面向量及应用
分析：利用平面向量的数量积运算求得
APk
•
APk+1
=（
AB
+k
BP1
）[
AB
+（k+1）
BP1
]=
AB
2+（2k+1）
AB
•
BP1
+k（k+1）
BP1
2=1-
2k+1
2n
+
k2+k
n2
，再利用数列求和即可得出结论．
解答： 解：
APk
•
APk+1
=（
AB
+k
BP1
）[
AB
+（k+1）
BP1
]=
AB
2+（2k+1）
AB
•
BP1
+k（k+1）
BP1
2=1-
2k+1
2n
+
k2+k
n2
，
∴Sn=
AB
•
AP1
+
AP1
•
AP2
+
AP2
•
AP3
…+
APn-1
•
AC
=
AB
•
AP1
+（n-1）-
3+5+7+…+(2n-1)
2n
+
(1+1)+(22+2)+…+(n2-n)
n2

=1-
1
2n
+n-1-
(n+1)(n-1)
2n
+
n(n-1)
2
+
n(n-1)(2n-1)
6
n2
=
5n2-2
6n
（n∈N+，n≥2）．
点评：本题主要考查平面向量的运算及数列求和的知识，考查学生的运算求解能力，属难题．
练习册系列答案
相关题目
设函数f（x）=（m-3）ex，g（x）=2ax+1+blnx，其中m，a，b∈R，x＞0．曲线g（x）在x=1处的切线方程为y=3x
（1）求函数g（x）的解析式；
（2）当k≤0时，求h（x）=
1
2
kx2+g（x）的单调区间；
（3）若f（x）的图象恒在g（x）图象的上方，求m的取值范围．
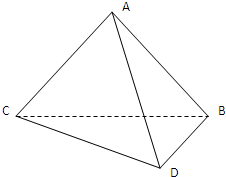如图，平面ABC⊥平面DBC，已知AB=AC，BC=6，∠BAC=∠DBC=90°，∠BDC=60° 
（1）求证：平面ABD⊥平面ACD；
（2）求二面角A-CD-B的平面角的余弦值；
（3）记经过直线AD且与BC平行的平面为α，求点B到平面α的距离．
一个袋子中有3个红球和2个黄球，5个球除颜色外完全相同，甲、乙两人先后不放回地从中各取1个球．规定：若两人取得的球的颜色相同则甲获胜，否则乙获胜．
（1）求两个人都取到黄球的概率；
（2）计算甲获胜的概率．
如图，一艘轮船在某海岛附近的海上匀速直线航行，海岛上一观察哨A在上午11时测得轮船在海岛北偏东60°的B处，12时20分测得轮船在海岛北偏西60°的C处，12时40分轮船到达位于海岛正西方且距离海岛5海里的D港口．
（Ⅰ）求证：S△ABC=4S△ACD；
（Ⅱ）求轮船的速度（单位：海里/小时）．
已知函数f（x）=sin（2ωx+
π
6
）（ω＞0），直线x=x1，x=x2是y=f（x）图象的任意两条对称轴，且|x1-x2|的最小值为
π
2
．
（1）求函数f（x）的单调增区间；
（2）求使不等式f（x）≥
3
2
的x的取值范围．
（3）若f（α）=
1
3
，α∈[-
π
3
，
π
6
]，求f（α+
π
6
）的值．
已知
a
=（1，-1），
b
=（λ，1），
（1）当
a
⊥
b
时，求λ的值．
（2）若
a
与
b
的夹角α为钝角，求λ的取值范围．
已知F为抛物线E：y2=2px（P＞0）的焦点，抛物线上点G的横坐标为2，且满足|GF|=3．
（Ⅰ）求抛物线E的方程；
（Ⅱ）M点的坐标为（2，0），过点F作斜率为1K的直线与抛物线交于A、B两点，A、B两点的横坐标均不为2，连结AM、BM并延长交抛物线于C、D两点，设直线CD的斜率为k2，判断
k1
k2
是否为定值？若是，求出该定值；若不是，请说明理由．
已知f（x）=
log2x    x＞0
4x      x≤0
，则f[f（
1
4
）]=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网