题目内容
3.若先将函数y=sin(4x+$\frac{π}{6}$)图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再将所得图象向左平移$\frac{π}{6}$个单位,则所得函数图象的一条对称轴的方程是( )| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律可得得函数图象对应的函数解析式为y=cos2x,再利用余弦函数的图象的对称性求得所得函数图象的一条对称轴方程.
解答 解:函数y=sin(4x+$\frac{π}{6}$)的图象上各点的纵坐标不变横坐标伸长到原来的2倍,所得图象的函数解析式为:y=sin(2x+$\frac{π}{6}$),图象再向左平移$\frac{π}{6}$个单位,
所得图象的函数解析式为:y=sin[2(x+$\frac{π}{6}$)+$\frac{π}{6}$]=sin(2x+$\frac{π}{2}$)=cos2x.
令2x=kπ,k∈Z,可解得函数对称轴方程为:x=$\frac{kπ}{2}$,k∈Z,
当k=1时,x=$\frac{π}{2}$是函数的一条对称轴.
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
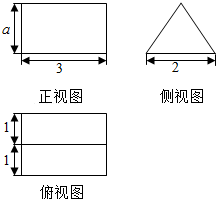 如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.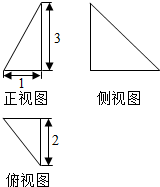
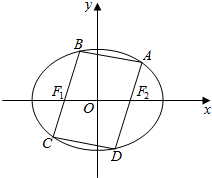 如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.
如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.