题目内容
8.先把函数y=cosx的图象上所有点向右平移$\frac{π}{3}$个单位,再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得到的函数图象的解析式为( )| A. | y=cos(2x+$\frac{π}{3}$) | B. | y=cos(2x-$\frac{π}{3}$) | C. | y=cos($\frac{1}{2}$x+$\frac{π}{3}$) | D. | y=cos($\frac{1}{2}$x-$\frac{π}{3}$) |
分析 利用导公式以及函数y=Asin(ωx+φ)的图象变换规律,可以求得变换后的函数的解析式.
解答 解:将函数y=cosx的图象向右平移$\frac{π}{3}$个单位长度,
可得函数y=cos(x-$\frac{π}{3}$)的图象;
再将所得图象的所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),
可得到的函数y=cos(2x-$\frac{π}{3}$)的图象,
故选:B.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
19.已知O为坐标原点,A,B两点的坐标均满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$,设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,则sinθ的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{4\sqrt{65}}{65}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
16.如图的程序框图表示算法的运行结果是( )


| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
3.sin(-$\frac{9π}{2}$)的值为( )
| A. | 1 | B. | -1 | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |
17.若4≤a≤8,0≤b≤2,则a+b的取值范围是( )
| A. | (4,10) | B. | [4,10] | C. | (6,8) | D. | [6,8] |
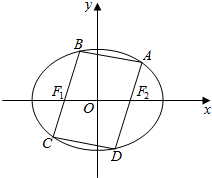 如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.
如图,已知四边形ABCD是椭圆3x2+4y2=12的内接平行四边形,且BC,AD分别经过椭圆的焦点F1,F2.