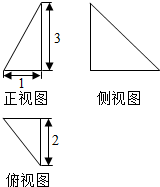
题目内容
7.在平面直角坐标系中,点P是直线l:x=-$\frac{1}{2}$上一动点,定点F($\frac{1}{2}$,0),点Q为PF的中点,动点M满足$\overrightarrow{MQ}$•$\overrightarrow{PF}$=0,$\overrightarrow{MP}$=λ$\overrightarrow{OF}$(λ∈R),过点M作圆(x-3)2+y2=2的切线,切点分别为S,T,则满足|ST|的最小值为$\frac{2\sqrt{30}}{5}$.分析 由题意首先求出M的轨迹方程,然后在M满足的曲线上设点,只要求曲线上到圆心的距离的最小值,即可得到|ST|的最小值.
解答 解:设M坐标为 M(x,y),由MP⊥l知 P(-$\frac{1}{2}$,y),
由点Q为PF的中点知 Q(0,$\frac{y}{2}$),
又因为QM⊥PF,QM、PF斜率乘积为-1,即 $\frac{y-\frac{y}{2}}{x}$=-$\frac{-\frac{1}{2}-\frac{1}{2}}{y}$,
解得:y2=2x,
∴M的轨迹是抛物线,
设M(y2,$\sqrt{2}$y),到圆心(3,0)的距离为d,d2=(y2-3)2+2y2=y4-4y2+9=(y2-2)2+5,
∴y2=2时,dmin=$\sqrt{5}$,此时的切线长为$\sqrt{5-2}=\sqrt{3}$,
∴|ST|的最小值为2×$\frac{\sqrt{3}×\sqrt{2}}{\sqrt{5}}$=$\frac{2\sqrt{30}}{5}$.
故答案为:$\frac{2\sqrt{30}}{5}$.
点评 本题考查了抛物线轨迹方程的求法以及与圆相关的距离的最小值求法,属于中档题.

练习册系列答案
相关题目
2.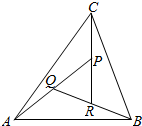 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )| A. | $\frac{2}{7},\frac{4}{7}$ | B. | $\frac{1}{2},\frac{1}{4}$ | C. | $\frac{1}{6},\frac{2}{7}$ | D. | $\frac{1}{6},\frac{3}{7}$ |
19.已知O为坐标原点,A,B两点的坐标均满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$,设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ,则sinθ的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{4\sqrt{65}}{65}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
16.如图的程序框图表示算法的运行结果是( )


| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
17.若4≤a≤8,0≤b≤2,则a+b的取值范围是( )
| A. | (4,10) | B. | [4,10] | C. | (6,8) | D. | [6,8] |