Question

关于两条不同的直线m、n与两个不同的平面α、β，有下列四个命题：
①若m∥α，n∥β且α∥β，则m∥n；
②若m∥α，n⊥β且α⊥β，则m∥n；
③若m?α，n?β且α⊥β，则m⊥n；
④若m⊥α，n⊥β且α⊥β，则m⊥n．
其中假命题有（　　）

• A、1个
• B、2个
• C、3个
• D、4个

Answer 1

考点：空间中直线与直线之间的位置关系

专题：计算题,空间位置关系与距离

分析：对四个命题，利用空间中线线、线面、面面间的位置关系，分别判断能求出结果．

解答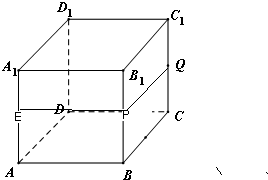： 解：对于①，在正方体ABCD-A₁B₁C₁D₁中，
平面ABCD∥平面A₁B₁C₁D₁，
A₁D₁∥平面ABCD，AD∥平面A₁B₁C₁D₁，A₁D₁∥AD；
EP∥平面ABCD，PQ∥平面A₁B₁C₁D₁，EP∩PQ=P；
A₁D₁∥平面ABCD，PQ∥平面A₁B₁C₁D₁，A₁D₁与PQ异面．
综上，直线m，n与平面α，β，m∥α，n∥β且α∥β，
则直线m，n的位置关系为平行或相交或异面．故①为假命题；
当m?β时，则m⊥n，故②为假命题；
∵m?α，n?β，且α⊥β，∴根据当m⊥β，可以推出直线m垂直于β内的所有条件，可以得到垂直与直线n，故③为假命题；
由m⊥α，n⊥β且α⊥β，则m与n一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m与n相交，
且设m与n确定的平面为γ，则γ与α和β的交线所成的角即为α与β所成的角，因为α⊥β，所以m与n所成的角为90°，故④正确
故选：C．

点评：本题考查两直线位置关系的判断，是中档题，解题时要注意空间思维能力的培养．