已知向量$\overrightarrow a.\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=2$.且$\overrightarrow a•({\overrightarrow b-\overrightarrow a})=-6$.则$\overrightarrow a.\overrightarrow b$ 题目和参考答案——青夏教育精英家教网—

题目内容

1．已知向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=2$，且$\overrightarrow a•（{\overrightarrow b-\overrightarrow a}）=-6$，则$\overrightarrow a，\overrightarrow b$的夹角是$\frac{2π}{3}$．

分析利用向量的数量积转化求解向量的夹角即可．

解答解：向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=2$，且$\overrightarrow a•（{\overrightarrow b-\overrightarrow a}）=-6$，
可得$\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{a}}^{2}$=-6，
$2×2×cos＜\overrightarrow{a}，\overrightarrow{b}＞$-4=-6，
可得cos$＜\overrightarrow{a}，\overrightarrow{b}＞$=-$\frac{1}{2}$．
则$\overrightarrow a，\overrightarrow b$的夹角是：$\frac{2π}{3}$．
故答案为：$\frac{2π}{3}$．

点评本题考查向量的数量积的运算，向量的夹角的求法，考查计算能力．

练习册系列答案

12．已知{a_n}是公差为1的等差数列，a₃+a₇=10
（1）求数列{a_n}的通项公式；
（2）设$b_n=2^{a_n}+a_n$，求数列{b_n}的前n项和T_n．

9．已知函数f（x）=sin（x+$\frac{π}{6}$），其中x∈[-$\frac{π}{3}$，$\frac{π}{2}$]，则f（x）的值域是[-$\frac{1}{2}$，1]．

16．若X～B（5，0.5），则P（X≥4）=$\frac{3}{16}$．

6．已知向量$\overrightarrow a=（{1，2sinθ}），\overrightarrow b=（{sin（{θ+\frac{π}{3}}），1}），θ∈R$．
（1）若$\overrightarrow a⊥\overrightarrow b$，求tanθ的值；
（2）若$\overrightarrow a∥\overrightarrow b$，且$θ∈[{0，\frac{π}{2}}]$，求角θ．

13．

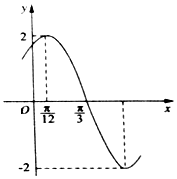已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，下列说法正确的是（　　）

	A．	函数f（x）的图象关于直线x=-$\frac{2π}{3}$对称
	B．	函数f（x）的图象关于点（-$\frac{11π}{12}$，0）对称
	C．	若方程f（x）=m在[-$\frac{π}{2}$，0]上有两个不相等的实数根，则实数m∈（-2，-$\sqrt{3}$]
	D．	将函数f（x）的图象向左平移$\frac{π}{6}$个单位可得到一个偶函数

7．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点到右焦点的距离为$\sqrt{3}$+$\sqrt{2}$，椭圆上的点到右焦点的距离的最小值为$\sqrt{3}$-$\sqrt{2}$．
（1）求椭圆C的方程；
（2）设斜率为1的直线l经过椭圆上顶点，并与椭圆交于A，B两点，求|AB|．

8．$g（x）=x+\frac{1}{x}$上各点处的切线倾斜角为α，则α的取值范围（　　）

$[{0，\frac{π}{4}}）∪（{\frac{3}{4}π，π}）$

D．

$[{0，\frac{π}{4}}）∪（{\frac{π}{2}，π}）$

试题分类