题目内容
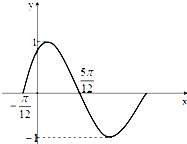 函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<
函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<| π |
| 2 |
(1)f(x)的解析式;
(2)f(x)的单调增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)令2kπ-
≤2x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.
(2)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解答:
解:(1)由函数的图象可得A=1,
T=
•
=
-(-
),求得ω=2.
再由五点法作图可得2×(-
)+Φ=0,求得Φ=
,
∴函数y=sin(2x+
).
(2)令2kπ-
≤2x+
≤2kπ+
,k∈z,求得kπ-
≤x≤kπ+
,k∈z,
故函数的增区间为[kπ-
,kπ+
],k∈z.
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| 5π |
| 12 |
| π |
| 12 |
再由五点法作图可得2×(-
| π |
| 12 |
| π |
| 6 |
∴函数y=sin(2x+
| π |
| 6 |
(2)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
故函数的增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的增区间,属于基础题.

练习册系列答案
相关题目
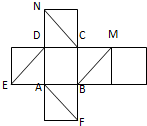 如图是正方体的平面展开图,在这个正方体中;
如图是正方体的平面展开图,在这个正方体中;(1)CN与AF平行;
(2)CN与BE是异面直线;
(3)CN与BM成60°;
(4)DE与BM垂直.
以上四个命题中,正确命题的序号是( )
| A、(1)(2)(3) |
| B、(2)(4) |
| C、(3)(4) |
| D、(3) |
 用长为18的钢条围成一个长方体形状的框架,设长方体的宽为x,长为2x,其体积为y
用长为18的钢条围成一个长方体形状的框架,设长方体的宽为x,长为2x,其体积为y 已知函数f(x)=|x2-2x|.
已知函数f(x)=|x2-2x|.