题目内容
观察不等式sin2α+cos2(α+30°)+sinαcosα(α+30°)=
;
sin2α+cos2(α+45°)+
sinαcosα(α+45°)=
;
sin2α+cos2(α+60°)+
sinαcosα(α+60°)=
;
sin2α+cos2(α+90°)+2sinαcosα(α+90°)=0.
可猜想得出结论:sin2α+cos2(α+75°)+ sinαcosα(α+75°)=
.
| 3 |
| 4 |
sin2α+cos2(α+45°)+
| 2 |
| 1 |
| 2 |
sin2α+cos2(α+60°)+
| 3 |
| 1 |
| 4 |
sin2α+cos2(α+90°)+2sinαcosα(α+90°)=0.
可猜想得出结论:sin2α+cos2(α+75°)+
2-
| ||
| 4 |
考点:归纳推理
专题:推理和证明
分析:分析观察得到等式的左边第三项的系数为2倍的第二项中α加的度数的正弦,从而得到答案.
解答:
解:由于sin2α+cos2(α+30°)+sinαcosα(α+30°)=
,
即为sin2α+cos2(α+30°)+2sin30°sinαcosα(α+30°)=
;
sin2α+cos2(α+45°)+
sinαcosα(α+45°)=
,
即为sin2α+cos2(α+45°)+2sin45°sinαcosα(α+45°)=
;
sin2α+cos2(α+90°)+2sinαcosα(α+90°)=0,
即为sin2α+cos2(α+90°)+2sin90°sinαcosα(α+90°)=0.
故sin2α+cos2(α+75°)+2sin75°sinαcosα(α+75°)=
,
即为sin2α+cos2(α+75°)+
sinαcosα(α+75°)=
.
故答案为:
.
| 3 |
| 4 |
即为sin2α+cos2(α+30°)+2sin30°sinαcosα(α+30°)=
| 3 |
| 4 |
sin2α+cos2(α+45°)+
| 2 |
| 1 |
| 2 |
即为sin2α+cos2(α+45°)+2sin45°sinαcosα(α+45°)=
| 1 |
| 2 |
sin2α+cos2(α+90°)+2sinαcosα(α+90°)=0,
即为sin2α+cos2(α+90°)+2sin90°sinαcosα(α+90°)=0.
故sin2α+cos2(α+75°)+2sin75°sinαcosα(α+75°)=
2-
| ||
| 4 |
即为sin2α+cos2(α+75°)+
| ||||
| 2 |
2-
| ||
| 4 |
故答案为:
| ||||
| 2 |
点评:本题考查归纳推理及应用,注意观察等式的特点是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
满足sinx≥
的x的集合为( )
| 1 |
| 2 |
A、{x|2kπ+
| ||||
B、{x|2kπ+
| ||||
C、{x|2kπ-
| ||||
D、{x|2kπ-
|
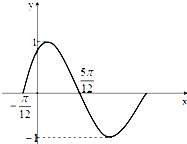 函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<
函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<