题目内容
 已知函数f(x)=|x2-2x|.
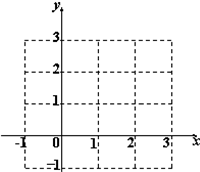
已知函数f(x)=|x2-2x|.(1)在给出的坐标系中作出y=f(x)的图象;
(2)用定义法证明f(x)在区间[2,+∞)上的单调性.
考点:函数的图象
专题:函数的性质及应用
分析:(1)首先取绝对值,转化为分段函数,画图即可.
(2)根据函数单调性的定义加以证明即可.
(2)根据函数单调性的定义加以证明即可.
解答:
解:(1)f(x)=|x2-2x|=
,
则y=f(x)的图象如图所示

(2)f(x)在区间[2,+∞)上的单调性.
则f(x)=x2-2x,x∈[2,+∞),
证明:设x1,x2∈[2,+∞),且设x1<x2,
则f(x1)-f(x2)=x12-2x1-x22+2x2=(x1+x2-2)(x1-x2),
∵x1,x2∈[2,+∞),且设x1<x2,
∴x1-x2<0,x1+x2-2>0,
∴f(x1)-f(x2)<0,
∴f(x)在区间[2,+∞)上的单调递增.
|
则y=f(x)的图象如图所示

(2)f(x)在区间[2,+∞)上的单调性.
则f(x)=x2-2x,x∈[2,+∞),
证明:设x1,x2∈[2,+∞),且设x1<x2,
则f(x1)-f(x2)=x12-2x1-x22+2x2=(x1+x2-2)(x1-x2),
∵x1,x2∈[2,+∞),且设x1<x2,
∴x1-x2<0,x1+x2-2>0,
∴f(x1)-f(x2)<0,
∴f(x)在区间[2,+∞)上的单调递增.
点评:本题主要考查了绝对值函数的图象和函数的单调性,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
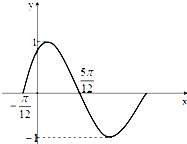 函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<
函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<