题目内容
已知等差数列{an}中，an=-2n+11
（1）求数列{an}的前n项和．
（2）当n为何值时，前n项和Sn有最大值，并求出最大值．
（1）求数列{an}的前n项和．
（2）当n为何值时，前n项和Sn有最大值，并求出最大值．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：（1）由等差数列的前n项和公式可求Sn；
（2）借助二次函数的性质可求；
（2）借助二次函数的性质可求；
解答：
解：（1）设等差数列{an}的前n项和为Sn，
则Sn=
=
=-n2+10n；
（2）由（1）知，Sn=-n2+10n=-（n-5）2+25，
当n=5时Sn有最大值为25．
则Sn=
| n(a1+an) |
| 2 |
| n(9-2n+11) |
| 2 |
（2）由（1）知，Sn=-n2+10n=-（n-5）2+25，
当n=5时Sn有最大值为25．
点评：该题考查等差数列的前n项和公式、数列的函数特性，属基础题，数列作为特殊的函数，解决数列问题时注意函数思想的应用．
练习册系列答案
教材全解字词句篇系列答案
相关题目
设a，b，c∈（-∞，0），则a+
，b+
，c+
（ ）
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |
当θ是第四象限时，两直线xsinθ+y
-a=0和x+y
+b=0的位置关系是（ ）
| 1+cosθ |
| 1-cosθ |
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、重合 |
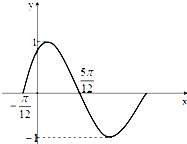函数y=Asin（ωx+Φ）（A＞0，ω＞0，|Φ|＜