题目内容
已知直线
x-2y-2
=0经过椭圆
+
=1(>b>0)的一个顶点E和一个焦点F.
(1)求椭圆的标准方程;
(2)若过焦点F作直线l,交椭圆于A,B两点,且椭圆上有一点C,使四边形AOBC恰好为平行四边形,求直线的斜率K.
| 6 |
| 6 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的标准方程;
(2)若过焦点F作直线l,交椭圆于A,B两点,且椭圆上有一点C,使四边形AOBC恰好为平行四边形,求直线的斜率K.
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)依题意,E(0,
),F(2,0),所以b=
,c=2,所以a2=10,即可得出椭圆的标准方程;
(2)可判断直线l⊥x轴时,不符合题意;设直线l的方程为y=k(x-2),点A(x1,y1),B(x2,y2),把l方程代入椭圆方程消掉y得x的二次方程,由四边形AOBC为平行四边形,得
+
=
,根据韦达定理可得点C的坐标,代入椭圆方程即可求得k值.
| 6 |
| 6 |
(2)可判断直线l⊥x轴时,不符合题意;设直线l的方程为y=k(x-2),点A(x1,y1),B(x2,y2),把l方程代入椭圆方程消掉y得x的二次方程,由四边形AOBC为平行四边形,得
| OA |
| OB |
| OC |
解答:
解:(1)依题意,E(0,
),F(2,0),
所以b=
,c=2,所以a2=10,
所以椭圆的标准方程为
+
=1;
(2)若直线l⊥x轴,则平行四边形AOBC中,点C与点O关于直线l对称,此时点C坐标为(2c,0).
因为2c>a,所以点C在椭圆外,所以直线l与x轴不垂直.
于是,设直线l的方程为y=k(x-2),点A(x1,y1),B(x2,y2),
y=k(x-2)代入椭圆方程,整理得(3+5k2)x2-20k2x+20k2-30=0,
所以x1+x2=
,所以y1+y2=-
.
因为四边形AOBC为平行四边形,所以
+
=
,
所以点C的坐标为(
,-
),
代入椭圆方程,解得k2=1,
所以k=±1.
| 6 |
所以b=
| 6 |
所以椭圆的标准方程为
| x2 |
| 10 |
| y2 |
| 6 |
(2)若直线l⊥x轴,则平行四边形AOBC中,点C与点O关于直线l对称,此时点C坐标为(2c,0).
因为2c>a,所以点C在椭圆外,所以直线l与x轴不垂直.
于是,设直线l的方程为y=k(x-2),点A(x1,y1),B(x2,y2),
y=k(x-2)代入椭圆方程,整理得(3+5k2)x2-20k2x+20k2-30=0,
所以x1+x2=
| 20k2 |
| 3+5k2 |
| 12k |
| 3+5k2 |
因为四边形AOBC为平行四边形,所以
| OA |
| OB |
| OC |
所以点C的坐标为(
| 20k2 |
| 3+5k2 |
| 12k |
| 3+5k2 |
代入椭圆方程,解得k2=1,
所以k=±1.
点评:本题考查直线方程、椭圆方程及其位置关系,考查向量的运算,考查学生分析解决问题的能力,考查分类讨论思想,属中档题.

练习册系列答案
相关题目
当θ是第四象限时,两直线xsinθ+y
-a=0和x+y
+b=0的位置关系是( )
| 1+cosθ |
| 1-cosθ |
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、重合 |
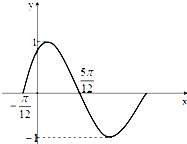 函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<
函数y=Asin(ωx+Φ)(A>0,ω>0,|Φ|<