题目内容
已知函数f(x)=9x-2•3x+3k-1(k为常数)
(1)求函数f(x)在(-∞,log3a]上的最小值(a为常数);
(2)若方程f(x)=0有两个实数根,求实数k的取值范围.
(1)求函数f(x)在(-∞,log3a]上的最小值(a为常数);
(2)若方程f(x)=0有两个实数根,求实数k的取值范围.
考点:导数在最大值、最小值问题中的应用,指数函数的图像与性质
专题:分类讨论,导数的综合应用
分析:(1)求出函数f(x)的导数f'(x),分别令大于0,小于0,写出f(x)的单调区间,对a讨论,分a=1,a>1,a<1三种情况,求出所给区间的最小值;
(2)通过换元转化为二次方程有两个不等的正根,由判别式大于0,根据根与系数的关系,列出不等式组,解出即可.
(2)通过换元转化为二次方程有两个不等的正根,由判别式大于0,根据根与系数的关系,列出不等式组,解出即可.
解答:
解:(1)函数f(x)=9x-2•3x+3k-1的导数f'(x)=9xln9-2•3xln3,
令f'(x)>0则3xln9•(3x-1)>0,即3x>1,即x>0,
令f'(x)<0则3xln9•(3x-1)<0,即3x<1,即x<0,
∴f(x)在(0,+∞)上递增,在(-∞,0)上递减.
∴①当a=1时,log3a=0,f(x)在区间(-∞,0]上有最小值3k-2,
②当a<1时,log3a<0,函数f(x)在(-∞,log3a]上递减,f(log3a)最小,且为a2-2a+3k-1,
③当a>1时,log3a>0,函数f(x)在(-∞,log3a]上的最小值f(0)且为3k-2,
∴当a≥1时,函数f(x)在(-∞,log3a]上的最小值为3k-2,
当a<1时,函数f(x)在(-∞,log3a]上的最小值为a2-2a+3k-1;
(2)令3x=t(t>0),则方程f(x)=0即为t2-2t+3k-1=0,
方程f(x)=0有两个实数根等价于方程t2-2t+3k-1=0有两个不等的正根,
∴
即
<k<
,
∴实数k的取值范围是(
,
).
令f'(x)>0则3xln9•(3x-1)>0,即3x>1,即x>0,
令f'(x)<0则3xln9•(3x-1)<0,即3x<1,即x<0,
∴f(x)在(0,+∞)上递增,在(-∞,0)上递减.
∴①当a=1时,log3a=0,f(x)在区间(-∞,0]上有最小值3k-2,
②当a<1时,log3a<0,函数f(x)在(-∞,log3a]上递减,f(log3a)最小,且为a2-2a+3k-1,
③当a>1时,log3a>0,函数f(x)在(-∞,log3a]上的最小值f(0)且为3k-2,
∴当a≥1时,函数f(x)在(-∞,log3a]上的最小值为3k-2,
当a<1时,函数f(x)在(-∞,log3a]上的最小值为a2-2a+3k-1;
(2)令3x=t(t>0),则方程f(x)=0即为t2-2t+3k-1=0,
方程f(x)=0有两个实数根等价于方程t2-2t+3k-1=0有两个不等的正根,
∴
|
| 1 |
| 3 |
| 2 |
| 3 |
∴实数k的取值范围是(
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题主要考查导数在函数中的应用:求单调区间,求最值,考查函数方程转换思想,以及分类讨论的重要思想方法,解题中应深刻领会.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
一个正三角形的外接圆的半径为1,向该圆内随机投一点P,点P恰好落在正三角形内的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
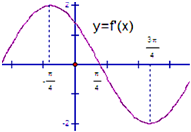 已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),其导函数f′(x)的部分图形如图所示,则函数f(x)的解析式( )A、f(x)=2sin(x+
| ||
B、f(x)=4sin(x+
| ||
C、f(x)=2sin(x+
| ||
D、f(x)=4sin(x+
|
设l,m,n为不同的直线,α,β为不同的平面,下列命题中正确的是( )
| A、若l∥α,m?α,则l∥m |
| B、若m∥n,n?α,则m∥α |
| C、若α不垂直于β,则α内不存在直线垂直于β |
| D、若α⊥β,l∥α,则l⊥β |
已知定义在R上的函数f(x)满足f(2-x)为奇函数,函数f(x+3)关于直线x=1对称,则下列式子一定成立的是( )
| A、f(x-2)=f(x) |
| B、f(x-2)=f(x+6) |
| C、f(x-2)•f(x+2)=1 |
| D、f(-x)+f(x+1)=0 |
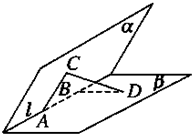 二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为
二面角α-l-β为60°,A、B是棱l上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l,且AB=AC=a,BD=2a,则CD的长为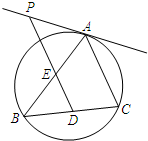 如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP∥AC,交AB于点E,交圆O