题目内容
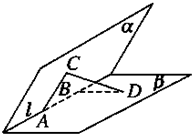二面角α-l-β为60°，A、B是棱l上的两点，AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，且AB=AC=a，BD=2a，则CD的长为考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：由已知条件推导出
2=（
+
+
）2=
2+
2+
2+2
•
，由此能求出CD的长．
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| BD |
| CA |
| BD |
解答：
解：∵二面角α-l-β为60°，A、B是棱l上的两点，
AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，
∴＜
，
＞=60°，且
•
=0，
•
=0，
∴
2=（
+
+
）2
=
2+
2+
2+2
•
=a2+a2+（2a）2+2a•2a•cos120°
=4a2，
∴CD的长=
=2a．
故答案为：2a．
AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，
∴＜
| AC |
| BD |
| AC |
| BA |
| AB |
| BD |
∴
| CD |
| CA |
| AB |
| BD |
=
| CA |
| AB |
| BD |
| CA |
| BD |
=a2+a2+（2a）2+2a•2a•cos120°
=4a2，
∴CD的长=
| 4a2 |
故答案为：2a．
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
F．
如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，则 
如图所示的算法框图中，语句“输出i”被执行的次数为（ ）
| A、32 | B、33 | C、34 | D、35 |