题目内容
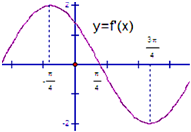已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），其导函数f′（x）的部分图形如图所示，则函数f（x）的解析式（ ）A、f（x）=2sin（x+
| ||
B、f（x）=4sin（x+
| ||
C、f（x）=2sin（x+
| ||
D、f（x）=4sin（x+
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由题意可得导函数f′（x）=Aωcos（ωx+φ）．根据周期求得ω，由f′（x）的最值求得A=2，根据五点法作图可得φ，从而得到函数的解析式．
解答：
解：∵函数f（x）=Asin（x+φ），∴其导函数f′（x）=Aωcos（ωx+φ）．
根据周期为
=2（
+
）=2π，∴ω=1，f′（x）=Acos（x+φ），∴A=2．
根据五点法作图可得1×（-
）+φ=
，可得φ=
，
∴函数f（x）=2sin（x+
），
故选：A．
根据周期为
| 2π |
| ω |
| 3π |
| 4 |
| π |
| 4 |
根据五点法作图可得1×（-
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
∴函数f（x）=2sin（x+
| 3π |
| 4 |
故选：A．
点评：本题主要考查利用y=Asin（ωx+φ）的图象特征，由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，从而求得函数的解析式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，则 如图所示的算法框图中，语句“输出i”被执行的次数为（ ）
| A、32 | B、33 | C、34 | D、35 |
在空间中，设α，β表示平面，m，n表示直线．则下列命题正确的是（ ）
| A、若m∥n，n⊥α，则m⊥α |
| B、若α⊥β，m?α，则m⊥β |
| C、若m上有无数个点不在α内，则m∥α |
| D、若m∥α，那么m与α内的任何直线平行 |
如图是计算
+
+
+…+
的值的一个程序框图，其中在判断框中应填入的条件是（ ）
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、i＜10 | B、i＞10 |
| C、i＜20 | D、i＞20 |
如图所示的程序框图输出的结果是S=720，则判断框内应填的条件是（ ）
| A、i≤7 | B、i＞7 |
| C、i≤9 | D、i＞9 |