题目内容
函数y=(
)2x+2×(
)x (x≤-1)的值域是 .
| 1 |
| 2 |
| 1 |
| 2 |
考点:二次函数在闭区间上的最值,函数的值域
专题:函数的性质及应用
分析:令t=(
)x,将函数换元为一元二次函数y=t2+2t,根据一元二次函数的单调区间直接求最值即可
| 1 |
| 2 |
解答:
解:∵y=(
)2x+2×(
)x(x≤-1),令(
)x=t,则t∈[2,+∞),∴原函数化为y=t2+2t=(t+1)2-1(t≥2)在[2,+∞)上是递增函数,∴y最小值=y(2)=8,故函数的值域是[8.+∞)
故答案为:[8.+∞)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:[8.+∞)
点评:本题考查复合函数的值域问题,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线l与直线y=1,直线x=5分别交于P,Q两点,PQ中点为M(1,-1),则直线l的斜率是( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、-2 |
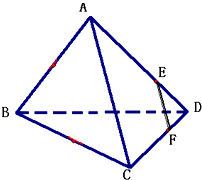 在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明:
在正四面体ABCD中,点F在CD上,点E在AD上,且DF:FC=DE:EA=2:3.证明: