题目内容
设A、B、C、D是空间四个不同的点，在下列命题中，不正确的是（ ）
| A、若直线AB与CD没有公共点，则AB∥CD |
| B、若AC与BD共面，则AD与BC共面 |
| C、若AC与BD是异面直线，则AD与BC是异面直线 |
| D、若AB=AC，DB=DC，则AD⊥BC |
考点：命题的真假判断与应用
专题：空间位置关系与距离,简易逻辑
分析：利用异面直线的定义判断A的正误；平面的基本性质判断B的正误；利用异面直线的定义判断C的正误；直接利用直线与平面垂直判断D的正误；
解答：
解：对于A，若直线AB与CD没有公共点，则AB∥CD，也可能是异面直线，∴A不正确．
对于B，当AC与BD共面时，不妨设AC与BD确定平面α，∵AC?α，BD?α，∴A∈α，D∈α，∴AD?α，同理BC?α，∴AD与BC共面，命题正确；
对于C，假设AD与BC共面，由A知，AC与BD也共面，这与AC与BD是异面直线矛盾，∴假设不成立，∴AD与BC是异面直线，∴命题正确；
对于D，如图，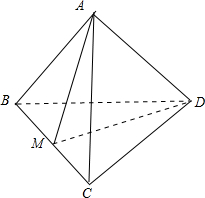
空间四边形ABCD中，AB=AC，DB=DC，取BC的中点M，连接AM、DM，AM⊥BC，DM⊥BC，∴BC⊥平面ADM，∴BC⊥AD，∴命题正确；
故选：A．
对于B，当AC与BD共面时，不妨设AC与BD确定平面α，∵AC?α，BD?α，∴A∈α，D∈α，∴AD?α，同理BC?α，∴AD与BC共面，命题正确；
对于C，假设AD与BC共面，由A知，AC与BD也共面，这与AC与BD是异面直线矛盾，∴假设不成立，∴AD与BC是异面直线，∴命题正确；
对于D，如图，
空间四边形ABCD中，AB=AC，DB=DC，取BC的中点M，连接AM、DM，AM⊥BC，DM⊥BC，∴BC⊥平面ADM，∴BC⊥AD，∴命题正确；故选：A．
点评：本题考查异面直线的定义的应用，共面直线与异面直线的区别，考查空间想象能力以及逻辑推理能力．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
下面的茎叶图表示柜台记录的一天销售额情况（单位：元），则销售额中的中位数是（ ）
| A、30.5 | B、31.5 |
| C、31 | D、32 |
已知O为坐标原点，P1、P2是双曲线
-
=1上的点．P是线段P1P2的中点，直线OP、P1P2的斜率分别为k1、k2，若2≤k1≤4，则k2的取值范围是（ ）
| x2 |
| 9 |
| y2 |
| 4 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
半径为1的球的内接正三棱柱（底面是正三角形的直棱柱）的侧面积为3
，则正三棱柱的高为（ ）
| 3 |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
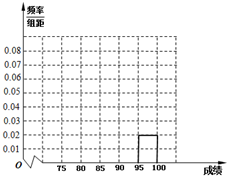某高中毕业学年，在高校自主招生期间，把学生的平时成绩按“百分制”折算，排出前n名学生，并对这n名学生按成绩分组，第一组[75，80），第二组[80，85），第三组[85，90），第四组[90，95），第五组[95，100]，如图为频率分布直方图的一部分，其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列，且第四组的人数为60．