题目内容
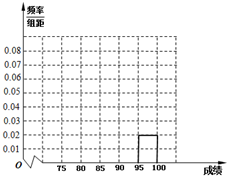 某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.(Ⅰ)请在图中补全频率分布直方图;
(Ⅱ)若Q大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若Q大学本次面试中有B、C、D三位考官,规定获得两位考官的认可即面试成功,且面试结果相互独立,已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
②若Q大学决定在这6名学生中随机抽取3名学生接受考官B的面试,第3组中有ξ名学生被考官B面试,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,分层抽样方法,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由第四组的人数能求出总人数,由此能补全频率分布直方图.
(Ⅱ)①设事件A=甲同学面试成功,由此利用独立事件概率公式能求出甲同学面试成功的概率.
②由题意得,ξ=0,1,2,3,分别求出其概率,由此能求出ξ的分布列和数学期望.
(Ⅱ)①设事件A=甲同学面试成功,由此利用独立事件概率公式能求出甲同学面试成功的概率.
②由题意得,ξ=0,1,2,3,分别求出其概率,由此能求出ξ的分布列和数学期望.
解答:
解:(Ⅰ)∵第四组的人数为60,
∴总人数为:5×60=300,

由直方图可知,第五组人数为:0.02×5×300=30人,
又
=15为公差,
∴第一组人数为:45人,第二组人数为:75人,第三组人数为:90人(4分)
(Ⅱ)①设事件A=甲同学面试成功,
则P(A)=
×
×
+
×
×
+
×
×
+
×
×
=
…..(8分)
②由题意得,ξ=0,1,2,3,
P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
分布列为:
E(ξ)=0×
+1×
+2×
+3×
=
…..(12分)
∴总人数为:5×60=300,

由直方图可知,第五组人数为:0.02×5×300=30人,
又
| 60-30 |
| 2 |
∴第一组人数为:45人,第二组人数为:75人,第三组人数为:90人(4分)
(Ⅱ)①设事件A=甲同学面试成功,
则P(A)=
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 4 |
| 15 |
②由题意得,ξ=0,1,2,3,
P(ξ=0)=
| ||||
|
| 1 |
| 20 |
P(ξ=1)=
| ||||
|
| 9 |
| 20 |
P(ξ=2)=
| ||||
|
| 9 |
| 20 |
P(ξ=3)=
| ||||
|
| 1 |
| 20 |
分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 20 |
| 9 |
| 20 |
| 9 |
| 20 |
| 1 |
| 20 |
| 3 |
| 2 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望,是中档题,是历年高考的必考题型.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是( )
| A、若直线AB与CD没有公共点,则AB∥CD |
| B、若AC与BD共面,则AD与BC共面 |
| C、若AC与BD是异面直线,则AD与BC是异面直线 |
| D、若AB=AC,DB=DC,则AD⊥BC |
在△ABC中,如果a,b,c分别是角A,B,C的对边,设命题p:(a2+b2)sin(A-B)=(a2-b2)sin(A+B);命题q:△ABC为直角三角形,那么命题p是命题q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
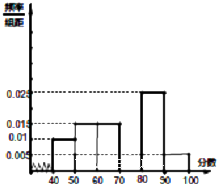 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),[90,100]后画出如下部分频率颁布直方图,观察图形的信息,回答下列问题: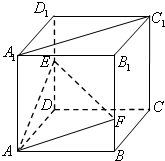 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.