题目内容
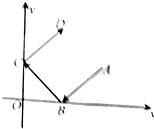 如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的
如图所示,光线从点A(2,1)出发,到x轴上的点 B后,被x轴反射到y轴上的C点,又被y轴反射,这时反射线恰好经过点D(1,2).
(1)求直线BC的方程;
(2)求线段BC的中垂线方程.
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:(1)求出点A(2,1)关于x轴的对称点A′(2,-1),点D(1,2)关于y轴的对称点D′(-1,2),然后由直线方程的两点式求得直线BC的方程;
(2)由(1)求得B,C的坐标,进一步求得BC的中点坐标,再求出直线BC的斜率,得到BC的中垂线的斜率,代入直线方程点斜式得答案.
(2)由(1)求得B,C的坐标,进一步求得BC的中点坐标,再求出直线BC的斜率,得到BC的中垂线的斜率,代入直线方程点斜式得答案.
解答:
解:(1)点A(2,1)关于x轴的对称点为A′(2,-1),
点D(1,2)关于y轴的对称点为D′(-1,2),
根据反射原理,A′,B,C,D′四点共线.
∴直线BC的方程为
=
,即x+y-1=0;
(2)由(1)得B(1,0),C(0,1).
∴BC的中点坐标为(
,
),kBC=-1.
∴线段BC的中垂线方程为y-
=x-
,即x-y=0.
点D(1,2)关于y轴的对称点为D′(-1,2),
根据反射原理,A′,B,C,D′四点共线.
∴直线BC的方程为
| y-(-1) |
| x-2 |
| 2-(-1) |
| -1-2 |
(2)由(1)得B(1,0),C(0,1).
∴BC的中点坐标为(
| 1 |
| 2 |
| 1 |
| 2 |
∴线段BC的中垂线方程为y-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了点关于直线的对称点的求法,考查了直线方程的两点式与点斜式,是基础题.

练习册系列答案
相关题目
已知集合M={y|y=3-x2,x∈R},N={x|y=
},则M∩(∁UN)=( )
(
|
| A、(-∞,0) | B、[0,3) |
| C、(0,3] | D、∅ |
下列函数是偶函数,且在(0,+∞)上是增函数的是( )
A、f(x)=(
| ||
B、f(x)=x
| ||
| C、f(x)=lnx | ||
| D、f(x)=-x2+4 |
下列直线中,与直线x-2y+1=0垂直的是( )
| A、2x-y-3=0 |
| B、x-2y+3=0 |
| C、2x+y+5=0 |
| D、x+2y-5=0 |
有2个兴趣小组,甲、乙、丙三位同学各参加其中一个小组,每位同学参加各个小组的可能性相同.则这三位同学参加同一个兴趣小组的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知α为第二象限角,sinα=
,则sin(π+2α)=( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|